Question

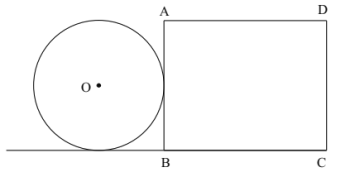
【题目】如图，在△ABO中，OA=OB，C是边AB的中点，以O为圆心的圆过点C.

（1）求证：AB与⊙O相切；

（2）若∠AOB=120°，AB=，求⊙O的面积.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

试题（1）由OA=OB，AC=BC，根据等腰三角形三线合一的性质可推出OC⊥AB，即AB是⊙O的切线 .

（2）由∠AOB=120°，AB=，根据等腰三角形三线合一的性质可推出∠AOC的度数和AC的长，根据锐角三角函数可求出OC的长，从而可求⊙O的面积.

试题解析：（1）如图，连接OC．

∵OA=OB，AC=BC，

∴OC⊥AB．

∴AB是⊙O的切线．

（2）∵OC是△ABO底边上的中线，∠AOB=120°，AB=，

∴∠AOC=60°，AC=.

∴在Rt△AOC中，.

∴.