题目内容
【题目】如图,某班研究性学习小组在一次综合实践活动中发现如下问题:在楼底的B处测得河对岸大厦上悬挂的条幅底端D的仰角为26°,在楼顶A处测得条幅顶端C的仰角为50°.若楼AB高度为18米,条幅CD长度为46米,请你帮助他们求出楼与大厦之间的距离BE及大厦的高度CE.(参考数据:sin26°≈0.44,sin50°≈0.77,tan26°≈0.49,tan50°≈1.19).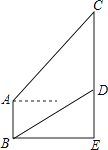
【答案】解: 过点A作AF⊥CE于点F,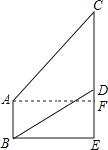
∵AB⊥BE,CE⊥BE,
∴四边形ABEF是矩形,
∴AF=BE,EF=AB=18m,
设BE=xm,
在Rt△BDE中,DE=BEtan∠DBE=BEtan26°=0.49x(m),
在Rt△ACF中,CF=AFtn∠CAF=AFtan50°=1.19x(m),
∵CD=CF+EF﹣DE,
∴1.19x+18﹣0.49x=46,
解得:x=40,
∴BE=40m,CE=CD+DE=46+0.49×40=65.6(m).
答:楼与大厦之间的距离BE为40m,大厦的高度CE为65.6m.
【解析】首先过点A作AF⊥CE于点F,易得四边形ABEF是矩形,然后设BE=xm,可得在Rt△BDE中,DE=BEtan∠DBE=BEtan26°=0.49x(m),在Rt△ACF中,CF=AFtn∠CAF=AFtan50°=1.19x(m),继而可得方程:1.19x+18﹣0.49x=46,解此方程即可求得答案.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目