题目内容
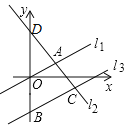
【题目】如图,在平面直角坐标系中,直线l1:y=![]() x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为﹣2.直线l2与y轴交于点D.
x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为﹣2.直线l2与y轴交于点D.
(1)求直线l2的解析式;
(2)求△BDC的面积.
【答案】直线l2的解析式为y=﹣![]() x+4;(2)16.
x+4;(2)16.
【解析】
(1)把x=2代入y=![]() x,得y=1,求出A(2,1).根据平移规律得出直线l3的解析式为y=
x,得y=1,求出A(2,1).根据平移规律得出直线l3的解析式为y=![]() x-4,求出B(0,-4)、C(4,-2).设直线l2的解析式为y=kx+b,将A、C两点的坐标代入,利用待定系数法即可求出直线l2的解析式;
x-4,求出B(0,-4)、C(4,-2).设直线l2的解析式为y=kx+b,将A、C两点的坐标代入,利用待定系数法即可求出直线l2的解析式;
(2)根据直线l2的解析式求出D(0,4),得出BD=8,再利用三角形的面积公式即可求出△BDC的面积.
(1)把x=2代入y=![]() x,得y=1,
x,得y=1,
∴A的坐标为(2,1).
∵将直线l1沿y轴向下平移4个单位长度,得到直线l3,
∴直线l3的解析式为y=![]() x-4,
x-4,
∴x=0时,y=-4,
∴B(0,-4).
将y=-2代入y=![]() x-4,得x=4,
x-4,得x=4,
∴点C的坐标为(4,-2).
设直线l2的解析式为y=kx+b,
∵直线l2过A(2,1)、C(4,-2),
∴![]() ,解得
,解得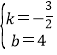 ,
,
∴直线l2的解析式为y=-![]() x+4;
x+4;
(2)∵y=-![]() x+4,
x+4,
∴x=0时,y=4,
∴D(0,4).
∵B(0,-4),
∴BD=8,
∴△BDC的面积=![]() ×8×4=16.
×8×4=16.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目