题目内容
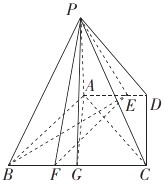
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC= ![]() ,点E在AD上,且AE=2ED.
,点E在AD上,且AE=2ED. 
(Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
(Ⅱ)若△PBC的面积是梯形ABCD面积的 ![]() ,求点E到平面PBC的距离.
,求点E到平面PBC的距离.
【答案】解:(Ⅰ)证明:∵AB⊥AC,AB=AC,∴∠ACB=45°, ∵底面ABCD是直角梯形,∠ADC=90°,AD∥BC,
∴∠ACD=45°,即AD=CD,
∴ ![]() ,
,
∵AE=2ED,CF=2FB,∴ ![]() ,
,
∴四边形ABFE是平行四边形,则AB∥EF,
∴AC⊥EF,
∵PA⊥底面ABCD,∴PA⊥EF,
∵PA∩AC=A,
∴EF⊥平面PAC,∵EF平面PEF,
∴平面PEF⊥平面PAC.
(Ⅱ)解:∵PA⊥底面ABCD,且AB=AC,∴PB=PC,
取BC的中点为G,连接AG,则AG⊥BC,AG=CD=1
设PA=x,连接PG,则 ![]() ,
,
∵侧面PBC的面积是底面ABCD的 ![]() 倍,
倍,
∴ ![]() ,即PG=2,求得
,即PG=2,求得 ![]() ,
,
∵AD∥BC,∴E到平面PBC的距离即时A到平面PBC的距离,
∵VA﹣PBC=VP﹣ABC , S△PBC=2S△ABC ,
∴E到平面PBC的距离为 ![]() .
.
【解析】(Ⅰ)已知点F在BC上,且CF=2FB,证明EF⊥平面PAC,即可证明:平面PEF⊥平面PAC;(Ⅱ)E到平面PBC的距离即时A到平面PBC的距离,利用VA﹣PBC=VP﹣ABC , 求点E到平面PBC的距离.
【考点精析】掌握平面与平面垂直的判定是解答本题的根本,需要知道一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目





