Question

【题目】如图，以直角三角形a、b、c为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足S1+S2=S3图形个数有（ ）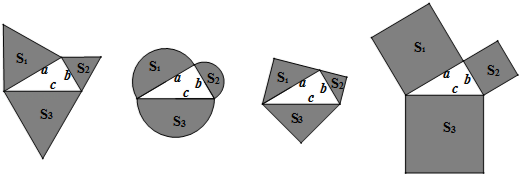
A.1
B.2
C.3
D.4

Answer 1

【答案】D
【解析】解：（1）S1= a2 ， S2= b2 ， S3= c2 ， ∵a2+b2=c2 ，
∴ a2+ b2= c2 ，
∴S1+S2=S3 ． （2）S1= a2 ， S2= b2 ， S3= c2 ，
∵a2+b2=c2 ，
∴ a2+ b2= c2 ，
∴S1+S2=S3 ． （3）S1= a2 ， S2= b2 ， S3= c2 ，
∵a2+b2=c2 ，
∴ a2+ b2= c2 ，
∴S1+S2=S3 ． （4）S1=a2 ， S2=b2 ， S3=c2 ，
∵a2+b2=c2 ，
∴S1+S2=S3 ．
综上，可得
面积关系满足S1+S2=S3图形有4个．
故选：D．
根据直角三角形a、b、c为边，应用勾股定理，可得a2+b2=c2 ． （1）第一个图形中，首先根据等边三角形的面积的求法，表示出3个三角形的面积；然后根据a2+b2=c2 ， 可得S1+S2=S3 ． （2）第二个图形中，首先根据圆的面积的求法，表示出3个半圆的面积；然后根据a2+b2=c2 ， 可得S1+S2=S3 ． （3）第三个图形中，首先根据等腰直角三角形的面积的求法，表示出3个等腰直角三角形的面积；然后根据a2+b2=c2 ， 可得S1+S2=S3 ． （4）第四个图形中，首先根据正方形的面积的求法，表示出3个正方形的面积；然后根据a2+b2=c2 ， 可得S1+S2=S3 ．