题目内容
【题目】定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
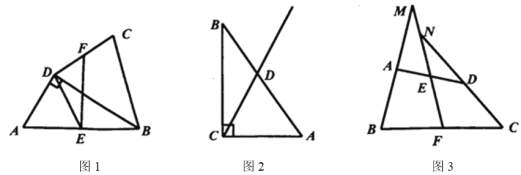
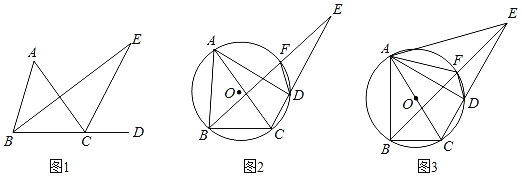
(1)如图1,∠E是△ABC中∠A的遥望角,若∠A=α,请用含α的代数式表示∠E.
(2)如图2,四边形ABCD内接于⊙O,![]() =
=![]() ,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.
,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.
(3)如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.
①求∠AED的度数;
②若AB=8,CD=5,求△DEF的面积.
【答案】(1)∠E=![]() α;(2)见解析;(3)①∠AED=45°;②
α;(2)见解析;(3)①∠AED=45°;②![]()
【解析】
(1)由角平分线的定义可得出结论;
(2)由圆内接四边形的性质得出∠FDC+∠FBC=180°,得出∠FDE=∠FBC,证得∠ABF=∠FBC,证出∠ACD=∠DCT,则CE是△ABC的外角平分线,可得出结论;
(3)①连接CF,由条件得出∠BFC=∠BAC,则∠BFC=2∠BEC,得出∠BEC=∠FAD,证明△FDE≌△FDA(AAS),由全等三角形的性质得出DE=DA,则∠AED=∠DAE,得出∠ADC=90°,则可求出答案;
②过点A作AG⊥BE于点G,过点F作FM⊥CE于点M,证得△EGA∽△ADC,得出![]() ,求出
,求出![]() ,设AD=4x,AC=5x,则有(4x)2+52=(5x)2,解得x=
,设AD=4x,AC=5x,则有(4x)2+52=(5x)2,解得x=![]() ,求出ED,CE的长,求出DM,由等腰直角三角形的性质求出FM,根据三角形的面积公式可得出答案.
,求出ED,CE的长,求出DM,由等腰直角三角形的性质求出FM,根据三角形的面积公式可得出答案.
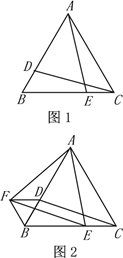
解:(1)∵BE平分∠ABC,CE平分∠ACD,
∴∠E=∠ECD﹣∠EBD=![]() (∠ACD﹣∠ABC)=
(∠ACD﹣∠ABC)=![]() α,
α,
(2)如图1,延长BC到点T,

∵四边形FBCD内接于⊙O,
∴∠FDC+∠FBC=180°,
又∵∠FDE+∠FDC=180°,
∴∠FDE=∠FBC,
∵DF平分∠ADE,
∴∠ADF=∠FDE,
∵∠ADF=∠ABF,
∴∠ABF=∠FBC,
∴BE是∠ABC的平分线,
∵![]() ,
,
∴∠ACD=∠BFD,
∵∠BFD+∠BCD=180°,∠DCT+∠BCD=180°,
∴∠DCT=∠BFD,
∴∠ACD=∠DCT,
∴CE是△ABC的外角平分线,
∴∠BEC是△ABC中∠BAC的遥望角.
(3)①如图2,连接CF,
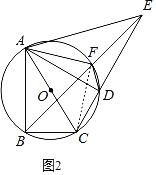
∵∠BEC是△ABC中∠BAC的遥望角,
∴∠BAC=2∠BEC,
∵∠BFC=∠BAC,
∴∠BFC=2∠BEC,
∵∠BFC=∠BEC+∠FCE,
∴∠BEC=∠FCE,
∵∠FCE=∠FAD,
∴∠BEC=∠FAD,
又∵∠FDE=∠FDA,FD=FD,
∴△FDE≌△FDA(AAS),
∴DE=DA,
∴∠AED=∠DAE,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠AED+∠DAE=90°,
∴∠AED=∠DAE=45°,
②如图3,过点A作AG⊥BE于点G,过点F作FM⊥CE于点M,
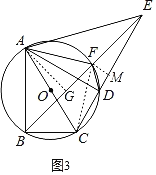
∵AC是⊙O的直径,
∴∠ABC=90°,
∵BE平分∠ABC,
∴∠FAC=∠EBC=![]() ∠ABC=45°,
∠ABC=45°,
∵∠AED=45°,
∴∠AED=∠FAC,
∵∠FED=∠FAD,
∴∠AED﹣∠FED=∠FAC﹣∠FAD,
∴∠AEG=∠CAD,
∵∠EGA=∠ADC=90°,
∴△EGA∽△ADC,
∴![]() ,
,
∵在Rt△ABG中,AG=![]() ,
,
在Rt△ADE中,AE=![]() AD,
AD,
∴![]() ,
,
在Rt△ADC中,AD2+DC2=AC2,
∴设AD=4x,AC=5x,则有(4x)2+52=(5x)2,
∴x=![]() ,
,
∴ED=AD=![]() ,
,
∴CE=CD+DE=![]() ,
,
∵∠BEC=∠FCE,
∴FC=FE,
∵FM⊥CE,
∴EM=![]() CE=
CE=![]() ,
,
∴DM=DE﹣EM=![]() ,
,
∵∠FDM=45°,
∴FM=DM=![]() ,
,
∴S△DEF=![]() DEFM=
DEFM=![]() .
.

 阅读快车系列答案
阅读快车系列答案