题目内容
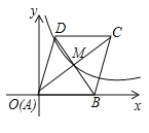
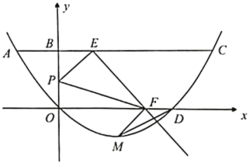
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x+3与x轴的一个交点为点A,与y轴的交点为点B,抛物线的对称轴l与x轴交于点,与线段AB交于点E,点D是对称轴l上一动点.
x+3与x轴的一个交点为点A,与y轴的交点为点B,抛物线的对称轴l与x轴交于点,与线段AB交于点E,点D是对称轴l上一动点.
(1)点A的坐标是 ,点B的坐标是 ;
(2)是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;
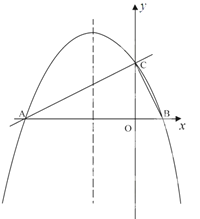
(3)如图2,抛物线的对称轴l向右平移与线段AB交于点F,与抛物线交于点G,当四边形DEFG是平行四边形且周长最大时,求出点G的横坐标.

【答案】(1)(6,0),(0,3);(2)存在,![]() 或
或![]() ;(3)G的横坐标为
;(3)G的横坐标为![]() .
.
【解析】
(1)令x=0,则y=3,令y=0,则x=6或﹣1,即可求解;
(2)分∠BDE=90、∠EBD=90°、∠BED=90°三种情况,分别求解即可;
(3)列出四边形的周长的函数表达式,即可求解.
解:(1)令x=0,则y=3,令y=0,则x=6或﹣1,
故点A、B的坐标分别为(6,0)、(0,3),
故答案为:(6,0);(0,3);
(2)存在,理由如下:
对称轴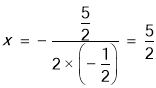 ,则
,则![]() ,
,
由点A、B的坐标得,直线AB的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
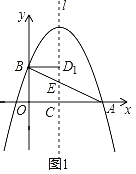
①当∠BDE=90°时,
∴BD∥CA,
∴△BDE∽△ACE,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②当∠EBD(D2)=90°时,
∵∠EBD2=∠ACE=90°,∠BED2=∠AEC,
∴△BED∽△CEA,
由①可知:![]() ;
;
同理:△BED1∽△D2BD1,
∴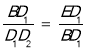 ,
,
即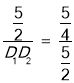 ,得D2D1=5,
,得D2D1=5,
∴![]() ;
;
③当∠BED=90°时,不合题意舍去.
综上所述![]() 或
或![]() .
.
(3)过点F作FH⊥CD于点H,
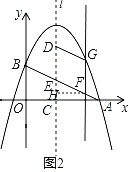
设![]() .
.
∴![]() ,
,
![]() .
.
∵BO∥CD,
∴∠OBA=∠CEF,
∵∠BOA=∠EHF=90°,
∴△BOA∽△EHF,,
∵![]() ,
,
则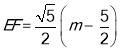 ,
,
设四边形的周长为CDEFG,则![]() ,
,
∵a=﹣1<0,
∴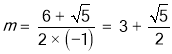 时平行四边形周长最大,
时平行四边形周长最大,
∴G的横坐标为![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目