题目内容
【题目】下列结论:①平面内3条直线两两相交,共有3个交点;②在平面内,若∠AOB =40°,∠AOC= ∠BOC,则∠AOC的度数为20°;③若线段AB=3, BC=2,则线段AC的长为1或5;④若∠a+∠β=180°,且∠a<∠β,则∠a的余角为![]() (∠β-∠a).其中正确结论的个数( )
(∠β-∠a).其中正确结论的个数( )
A.1个B.2个C.3个D.4个
【答案】A
【解析】
根据相交线的定义,角平分线的定义,线段的和差,余角和补角的定义进行判断找到正确的答案即可.
解:①平面内3条直线两两相交,如下图,
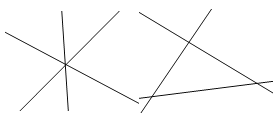
有1个(左图)或3个交点(右图),故错误;
②在平面内,若∠AOB=40°,∠AOC=∠BOC,如下图,
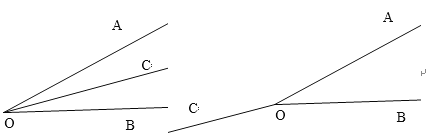
∠AOC的度数为20°(左图)或160°(右图),故错误;
③若线段AB=3,BC=2,因为点C不一定在直线AB上,所以无法求得AC的长度,故错误;
④若∠α+∠β=180°,则![]() ,则当∠a<∠β时,
,则当∠a<∠β时,![]() ,则
,则![]() ,故该结论正确.
,故该结论正确.
故正确的有一个,选:A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
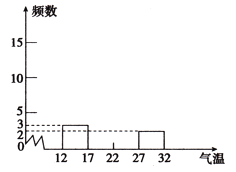
【题目】银川市2019年5月1日---20日的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19
解答下列问题:
(1)将下表补充完整:
气温分组 | 12≤x<17 | 17≤x<22 | 22≤x<27 | 27≤x<32 |
频数 | 3 | 2 | ||
百分比 | 15% | 25% |
(2)补全频数直方图