题目内容
（2010•宝安区一模）如图，菱形ABCD中，DE⊥AB于E，DF⊥BC于F．（1）求证：△ADE≌△CDF；
（2）若∠EDF=50°，求∠BEF的度数．
【答案】分析：（1）在直角△ADE和直角△CDF中，AD=CD，再证明Rt△ADE≌Rt△CDF；
（2）根据△ADE≌△CDF，可得DE=DF，即可求解．
解答：（1）证明：在△ADE和△CDF，
∵四边形ABCD是菱形，∴AD=CD，∠A=∠C，
又∵∠DFC=∠DEA=90°，
∴Rt△ADE≌Rt△CDF；
（2）解：由△ADE≌△CDF，∴DE=DF，
∴∠DEF=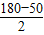
=65°，
∴∠BEF=90°-65°=25°．
点评：本题考查了菱形的性质及全等三角形的判断，难度不大，关键熟练掌握菱形的性质．
（2）根据△ADE≌△CDF，可得DE=DF，即可求解．
解答：（1）证明：在△ADE和△CDF，
∵四边形ABCD是菱形，∴AD=CD，∠A=∠C，
又∵∠DFC=∠DEA=90°，
∴Rt△ADE≌Rt△CDF；
（2）解：由△ADE≌△CDF，∴DE=DF，
∴∠DEF=
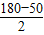=65°，∴∠BEF=90°-65°=25°．
点评：本题考查了菱形的性质及全等三角形的判断，难度不大，关键熟练掌握菱形的性质．
练习册系列答案
全能测控期末小状元系列答案
相关题目
（x-2）2-2与x轴分别交于O、A两点，将抛物线l1向上平移得到l2，过点A作AB⊥x轴交抛物线l2于点B，如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16，则抛物线l2的函数表达式为（ ）
（x-2）2+4
（x-2）2+3
（x-2）2+2
（x-2）2+1