题目内容
(2010•宝安区一模)“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
【答案】分析:(1)设商品的定价为x元,由这种商品的售价每上涨1元,其销售量就减少2件,列出等式求得x的值即可;
(2)设利润为y元,列出二次函数关系式,在售价不超过40元/件的范围内求得利润的最大值.
解答:解:(1)设商品的定价为x元,由题意,得
(x-20)[100-2(x-30)]=1600,
解得:x=40或x=60;
答:售价应定为40元或60元.
(2)设利润为y元,得:
y=(x-20)[100-2(x-30)](x≤40),
即:y=-2x2+200x-3200;
∵a=-2<0,
∴当x=-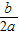 =-
=-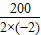 =50时,y取得最大值;
=50时,y取得最大值;
又x≤40,则在x=40时可取得最大值,
即y最大=1600.
答:售价为40元/件时,此时利润最大,最大为1600元.
点评:本题考查的是二次函数在实际生活中的应用,关键是对题意的正确理解.
(2)设利润为y元,列出二次函数关系式,在售价不超过40元/件的范围内求得利润的最大值.
解答:解:(1)设商品的定价为x元,由题意,得
(x-20)[100-2(x-30)]=1600,
解得:x=40或x=60;
答:售价应定为40元或60元.
(2)设利润为y元,得:
y=(x-20)[100-2(x-30)](x≤40),
即:y=-2x2+200x-3200;
∵a=-2<0,
∴当x=-
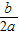 =-
=-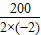 =50时,y取得最大值;
=50时,y取得最大值;又x≤40,则在x=40时可取得最大值,
即y最大=1600.
答:售价为40元/件时,此时利润最大,最大为1600元.
点评:本题考查的是二次函数在实际生活中的应用,关键是对题意的正确理解.

练习册系列答案
相关题目

 (x-2)2-2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2,过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
(x-2)2-2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2,过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
 (x-2)2+4
(x-2)2+4 (x-2)2+3
(x-2)2+3 (x-2)2+2
(x-2)2+2 (x-2)2+1
(x-2)2+1
