题目内容
 两个反比例函数y=
两个反比例函数y=| 3 |
| x |
| 6 |
| x |
| 3 |
| x |
3
3
.分析:求出N(m,
),根据平行线和N的坐标求出P2的横坐标是m,P1的纵坐标是
,代入y=
,求出P1、P2的坐标,求出NP2、NP1的值,即可求出NP1与NP2的积.
| 3 |
| m |
| 3 |
| m |
| 6 |
| x |
解答:解:N(m,n)在y=
上,
∴N(m,
),
∵NP2∥y轴,NP1∥x轴,
∴P2的横坐标是m,P1的纵坐标是
,
∵P1、P2在y=
上,
代入得:①y=
,
②
=
,∴x=2m,
∴P1(2m,
),P2(m,
),
∴NP2=
-
=
,NP1=2m-m=m,
∴NP1与NP2的积是
×m=3,
故答案为:3.
| 3 |
| x |
∴N(m,
| 3 |
| m |
∵NP2∥y轴,NP1∥x轴,
∴P2的横坐标是m,P1的纵坐标是
| 3 |
| m |
∵P1、P2在y=
| 6 |
| x |
代入得:①y=
| 6 |
| m |
②
| 3 |
| m |
| 6 |
| x |
∴P1(2m,
| 3 |
| m |
| 6 |
| m |
∴NP2=
| 6 |
| m |
| 3 |
| m |
| 3 |
| m |
∴NP1与NP2的积是
| 3 |
| m |
故答案为:3.
点评:本题考查了对一次函数图象上点的坐标特征及其应用的运用,关键是根据N的坐标求出P1、P2的坐标,主要考查学生运用性质进行推理的能力,题目比较典型,有一定的难度.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
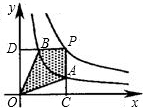 ,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( )
,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( ) 如图,两个反比例函数
如图,两个反比例函数
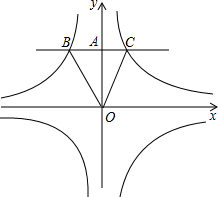 如图,已知反比例函数y=
如图,已知反比例函数y= 已知两个反比例函数
已知两个反比例函数