题目内容
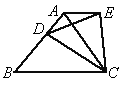
(2005 江苏苏州)如图所示,等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.

(1)求证:AE∥BC;
(2)如图所示,将(1)中等边△ABC的形状改成以BC为底边的等腰三角形,所作△EDC改成相似于△ABC.请问:是否仍有AE∥BC?证明你的结论.
答案:略
解析:
解析:
|
证明 ∵△ ABC与△EDC都是等边三角形,∴∠ ECD=∠ACB=60°.∴∠ ECD-∠ACD=∠ACB-∠ACD.即∠ ACE=∠BCD.又∵ AC=BC,EC=DC,∴△ ACE≌△BCD.∴∠ EAC=∠B=60°.∴∠ EAC=∠ACB.∴ AE∥BC.(2) 仍有AE∥BC.证明:∵△ EDC∽△ABC,∴  , ,
∠ ECD=∠ACB.∴∠ ECD=∠ACD=∠ACB-∠ACD.即∠ ACE=∠BCD.∴△ ACE∽△BCD.∴∠ EAC=∠B.∵在△ ABC中,AB=AC,∴∠ B=∠ACB.∴∠ EAC=∠ACB.∴ AE∥BC. |

练习册系列答案
相关题目
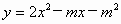 .
.


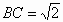 ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)