题目内容
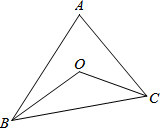
已知,如图,∠XOY=90°,点A、B分别在射线OX、OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
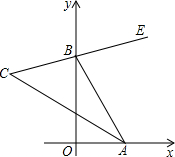

∠C的大小保持不变.理由:
∵∠ABY=90°+∠OAB,AC平分∠OAB,BE平分∠ABY,
∴∠ABE=
∠ABY=
(90°+∠OAB)=45°+
∠OAB,
即∠ABE=45°+∠CAB,
又∵∠ABE=∠C+∠CAB,
∴∠C=45°,
故∠ACB的大小不发生变化,且始终保持45°.
∵∠ABY=90°+∠OAB,AC平分∠OAB,BE平分∠ABY,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠ABE=45°+∠CAB,
又∵∠ABE=∠C+∠CAB,
∴∠C=45°,
故∠ACB的大小不发生变化,且始终保持45°.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目