题目内容
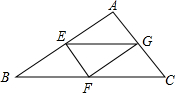如图，△ABC的三边长分别是6cm、8cm、10cm，现在分别取三边的中点E、F、G，顺次连接E、F、G，则△EFG的面积为________．
6 cm2
分析：根据三角形的中位线定理求出EF、FG、EG的长，根据勾股定理的逆定理求出∠EFG=90°，根据三角形的面积公式求出即可．
解答：∵E为AB的中点，F为BC的中点，G为AC的中点，
∴EG=
BC=5cm，
同理：FG=4cm，EF=3cm，
∵FG2+EF2=42+32=25，EG2=52=25，
∴EG2=EF2+FG2，
∴∠EFG=90°，
∴△EFG的面积是EF×FG=×3cm×4cm=6cm2，
故答案为：6cm2．
点评：本题考查了三角形的面积，勾股定理的逆定理，三角形的中位线等知识点的应用，关键是求出∠EFG=90°和求出△EFG的三边的长，通过做此题培养了学生运用定理进行推理和计算的能力，题型较好，难度不大．
分析：根据三角形的中位线定理求出EF、FG、EG的长，根据勾股定理的逆定理求出∠EFG=90°，根据三角形的面积公式求出即可．
解答：∵E为AB的中点，F为BC的中点，G为AC的中点，
∴EG=
BC=5cm，同理：FG=4cm，EF=3cm，
∵FG2+EF2=42+32=25，EG2=52=25，
∴EG2=EF2+FG2，
∴∠EFG=90°，
∴△EFG的面积是
EF×FG=×3cm×4cm=6cm2，故答案为：6cm2．
点评：本题考查了三角形的面积，勾股定理的逆定理，三角形的中位线等知识点的应用，关键是求出∠EFG=90°和求出△EFG的三边的长，通过做此题培养了学生运用定理进行推理和计算的能力，题型较好，难度不大．
练习册系列答案
相关题目
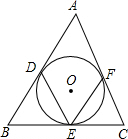如图，△ABC的三边分别切⊙O于D，E，F，若∠A=40°，则∠DEF=
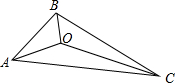如图，△ABC的三边AB、BC、AC的长分别为4，6，8，其三条角平分线将△ABC分成三个三角形，则S△OAB：S△OBC：S△OAC=
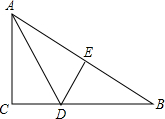如图，△ABC的三边长分别为AC=12，AB=15，BC=9．若将△ABC沿线段AD折叠，点C正好落在AB边上的点E处．求线段CD的长度．
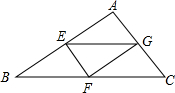如图，△ABC的三边长分别是6cm、8cm、10cm，现在分别取三边的中点E、F、G，顺次连接E、F、G，则△EFG的面积为