��Ŀ����
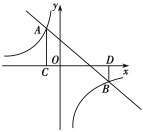
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() �͵�
�͵�![]() ��ֱ��
��ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() �͵�
�͵�![]() ��ֱ��
��ֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���߶�
���߶�![]() ��
��![]() �ij���-Ԫ���η���
�ij���-Ԫ���η���![]() ������(
������(![]() )��
)�� ![]() ����
����![]() �ĺ�����Ϊ3������������
�ĺ�����Ϊ3������������![]() ��ͼ����
��ͼ����![]() ��
��
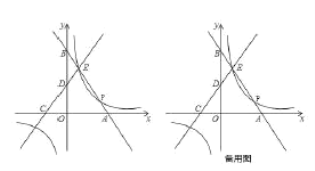
��1����ֱ��![]() �뷴��������ͼ���ϳ���
�뷴��������ͼ���ϳ���![]() �����һ����Ϊ
�����һ����Ϊ![]() ����
����![]() �����������
�����������![]() ��
��![]() ���ϣ�����
���ϣ�����![]() ��
��![]() ���ϣ���
���ϣ���![]() ����Сֵ��
����Сֵ��
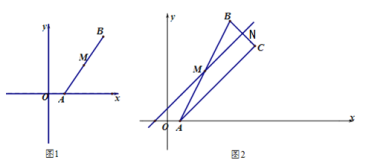
��2������![]() �������ᣮ�ϣ���ƽ���ڴ���һ��
�������ᣮ�ϣ���ƽ���ڴ���һ��![]() ��ʹ�Ե�
��ʹ�Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����Ǿ������߶�
Ϊ������ı����Ǿ������߶�![]() Ϊ���ε�һ���ߣ� ֱ��д������������
Ϊ���ε�һ���ߣ� ֱ��д������������![]() �����꣮
�����꣮
���𰸡���1��72��20����2��N�������Ϊ(9��![]() )��(9��
)��(9��![]() )��(10��12)
)��(10��12)
��������
��1���Ƚ�һԪ���η��̣��ó�0A, OC�����ɵõ�A,C���꣬�������OB,�ó�B�����꣬�������ֱ��AB����ʽ�����ɵó���E���꣬�������P���꣬��������IJ����������ECP�������������P����x ��ĶԳƵ�P��,������E����y��ĶԳƵ�E', P��E'����![]() ����Сֵ��
����Сֵ��
��2����ȷ����ֱ��CE����ʽ���ٹ���E��ֱ��CE�Ĵ������������ཻ��M, M��,���MM���Ľ���ʽ���������ݾ��ε����ʣ����ֱ��BN, CN, M'N�������ֱ�߽������꼴�ɣ�
��1�����߶�OA��OC�ij���һԪ���η��̵�![]() ����(OA>OC)��
����(OA>OC)��
��OC=6��OA=12��
��A(12,0),C(6,0)��
��OB=![]() OA=16��
OA=16��
��B(0,16)��
��ֱ��AB����ʽΪy=k��x+16��
��12k��+16=0��
��k��=![]() ��
��
��ֱ��AB����ʽΪy=![]() x+16��
x+16��
��AB��CD�ཻ�ڵ�E����E�ĺ�����Ϊ3��
��E(3,12)��
�߷���������![]() ��ͼ����E��
��ͼ����E��
��k=3��12=36��
��ͼ1��
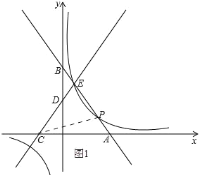
�ߵ�P��ֱ��AB�ϣ�
����P(m,![]() m+16)��
m+16)��
��(1)֪��k=36��
�෴������������ʽΪy=36x��
�ߵ�P���ڷ�����������ͼ���ϣ�
��m��(![]() m+16)=36��
m+16)=36��
��m=3(��)��m=9��
��P(9,4)��
��(1)֪,A(12,0),C(6,0),E(3,12)
��AC=18
��S��ECP=S��ECAS��PCA=12AC��|yE|12AC��|yP|=12AC��(|yE||yP|)=12��18��(124)=72��
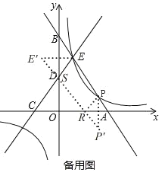
�籸��ͼ������P����x��ĶԳƵ㣬
��P(9,4)��
��P��(9,4)��
����E����y��ĶԳƵ㣬
��E(3,12)��
��E��(3,12)��
����P��E����x����R����y����S����ʱ��PR+RS+RE��С��
��Сֵ=P��E��=![]()
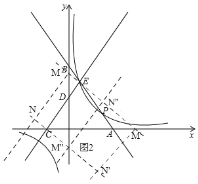
��2����ͼ2,��(1)֪,C(6,0),E(3,12)��
��ֱ��CE����ʽΪy=![]() x+8��
x+8��
���Ե�C��E��
�����E��MM����CE��
��ֱ��MM���Ľ���ʽΪy=![]() x+
x+![]() �ܣ�
�ܣ�
��M(0,![]() ).M��(19,0)��
).M��(19,0)��
����M��MN��CE��
��ֱ��MN����ʽΪy=![]() x+
x+![]() ,��
,��
����C��CN��MN��
��ֱ��CN�Ľ���ʽΪy=![]() x
x![]() ��
��
�������٢ڵ�,x=9,y=![]() ��
��
��N(9,![]() )��
)��
�ڹ���M����M��N����MM����ֱ��CN��N��
��ֱ��M��N���Ľ���ʽΪy=![]() x
x![]() �ۣ�
�ۣ�
�����ڢ۵ã�x=10��y=12��
��N��(10,12)��
�۹�M�����M���N����CN��MM����N��
��ֱ��CN�Ľ���ʽΪy=![]() x
x![]()
��M���N����Ľ���ʽΪy=![]() x
x![]() �ݣ�
�ݣ�
�����ܢݽ��,x=9,y=![]() ��
��
��N���(9,![]() )
)
������������N�������Ϊ(9,![]() )��(9,
)��(9,![]() )��(10,12)
)��(10,12)

 ��У����ϵ�д�
��У����ϵ�д�