题目内容
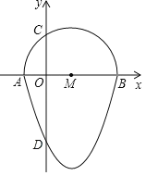
【题目】如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”，已知点
、
、
、
分别是“果圆”与坐标轴的交点，抛物线的解析式为
，
为半圆的直径，则这个“果圆”被
轴截得的弦
的长为_________．
【答案】
【解析】
连接CM，根据抛物线解析式求出OD=12，AO=2，BO=6，AB=8，M（2，0），利用勾股定理求出OC，即可得到CD的长度.
连接CM，
∵抛物线的解析式为
，
∴点D的坐标为（0，-12），
∴OD=12.
设y=0，则0=x2-4x-12，解得：x=-2或6，
∴A（-2，0），B（6，0）.
∴AO=2，BO=6，AB=8，M（2，0），
∴MC=4，OM=2，
在Rt△COM中，OC=
,
∴CD= OD+ OC=,
即这个“果圆”被y轴截得的线段CD的长，
故答案为：.
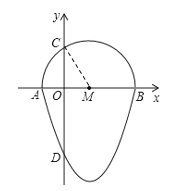
考前必练系列答案【题目】某校学生会干部对全校师生倡导的“武汉加油”的自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）．已知A、B两组捐款人数的比为1∶5．
组别 | 捐款额x（元） | 人数 |
A | 1≤x＜10 | a |
B | 10≤x＜20 | 100 |
C | 20≤x＜30 | |
D | 30≤x＜40 | |
E | 40≤x＜50 |
请结合以上信息解答下列问题．
（1）a＝ ，本次调查样本的容量是 ；
（2）先求出C组的人数，再补全“捐款人数分组统计图1”；
（3）根据统计情况，估计该校参加捐款的5000名学生有多少人捐款在20至50元之间．
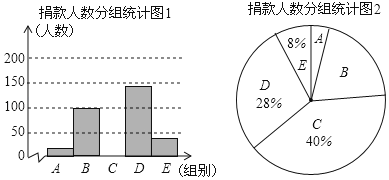
【题目】为了解某地区企业信息化发展水平，从该地区中随机抽取50家企业调研，针对体现企业信息化发展水平的A和B两项指标进行评估，获得了它们的成绩（十分制），并对数据（成绩）进行整理、描述和分析．下面给出了部分信息．
a．A项指标成绩的频数分布直方图如下（数据分成6组：
，
，
，
，
，
）：
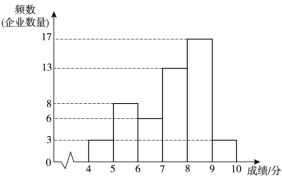
b．A项指标成绩在这一组的是：
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c．
两项指标成绩的平均数、中位数、众数如下：
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息，回答下列问题：
（1）写出表中m的值
（2）在此次调研评估中，某企业A项指标成绩和B项指标成绩都是7.5分，该企业成绩排名更靠前的指标是______________（填“A”或“B”），理由是_____________；
（3）如果该地区有500家企业，估计A项指标成绩超过7.68分的企业数量．
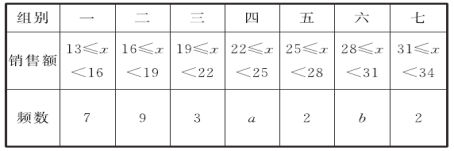
【题目】某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每位营业员在某月的销售额(单位：万元)，数据如下：
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组，并整理、描述和分析如下：
频数分布表
数据分析表
平均数 | 众数 | 中位数 |
20.3 | c | 18 |
请根据以上信息解答下列问题：
(1)填空：a＝____，b＝_____，c＝_____；
(2)若将月销售额不低于25万元确定为销售目标，则有______位营业员获得奖励；
(3)若想让一半左右的营业员都能达到销售目标，你认为月销售额定为多少合适？说明理由．
