题目内容
【题目】已知抛物线y＝ax2+bx经过点A（﹣4，﹣4）和点B（m，0），且m≠0．
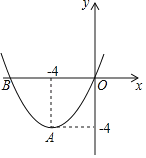
（1）若该抛物线的对称轴经过点A，如图，请根据观察图象说明此时y的最小值及m的值；
（2）若m＝4，求抛物线的解析式（也称关系式），并判断抛物线的开口方向．
【答案】（1）y的最小值为﹣4，m＝﹣8；（2）
，开口向下．
【解析】
（1）根据二次函数的性质得此时y的最小值，利用对称性得到B（﹣8，0），从而确定m的值；
（2）设交点式y＝ax（x﹣4），再把A（﹣4，﹣4）代入求得a＝
，从而得到抛物线解析式，利用二次函数的性质确定抛物线开口方向．
解：（1）∵该抛物线的对称轴经过点A，
∴点A（﹣4，﹣4）为抛物线的顶点，对称轴为直线x＝﹣4，
∴此时y的最小值为﹣4；
∵点B和原点为抛物线的对称点，
∴B（﹣8，0），
∴m＝﹣8；
（2）当m＝4时，即B（4，0），
设抛物线解析式为y＝ax（x﹣4），
把A（﹣4，﹣4）代入得﹣4＝a×（﹣4）×（﹣4﹣4），解得a＝，
∴抛物线解析式为y＝x（x﹣4），
即y＝x2+
x，
∵a＜0，
∴抛物线开口向下．
练习册系列答案
相关题目
