题目内容
【题目】如图所示.某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其余两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,每平方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.
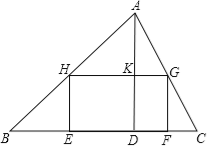
(1)当FG长为多少米时,种草的面积与种花的面积相等?
(2)当矩形EFGH的边FG为多少米时,△ABC空地改造总投资最小,最小值为多少?
【答案】(1)40;(2)FG=60时,△ABC空地改造总投资最小,最小值为26400.
【解析】
(1)可利用相似分别表示出相应的三角形的底与高,让面积相等即可;
(2)把相应的总投资用含x的代数式表示出后,求出二次函数的最值即可.
解:(1)设FG=x米,则AK=(80﹣x)米.
由△AHG∽△ABC,BC=120,AD=80,
可得:![]() ,
,
∴HG=![]() ,BE+FC=120﹣(
,BE+FC=120﹣(![]() )=
)=![]() ,
,
∴![]() ,
,
解得![]() .
.
∴当FG的长为40米时,种草的面积和种花的面积相等.
(2)设改造后的总投资为W元.
则W=![]()
=![]() ,
,
∵二次项系数6>0,0<x≤80,
∴当x=20时,W最小=26400.
答:当矩形EFGH的边FG长为20米时,空地改造的总投资最小,最小值为26400元.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目