题目内容
【题目】如图,长方形纸片ABCD,点E在边AB上,M、N分别在射线BC和射线AD上,连接EM,EN,将三角形MBE沿EM折叠(把物体的一部分翻转和另一部分贴拢),点B落在点B’处;将三角形NAE沿EN折叠,点A落在点A’处.
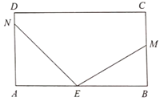
(1)若![]() ,
,![]() ,用直尺、量角器画出射线EB’与EA’;
,用直尺、量角器画出射线EB’与EA’;
(2)若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
【答案】(1)作图见解析;(2)30°;(3)∠A'EB'=180°-2(α+β)或2(α+β)-180°.
【解析】
(1)根据已知作图即可;
(2)由折叠的性质得到∠AEN=∠A'EN,∠BEM=∠B'EM,根据平角的定义得到2∠AEN+2∠BEM+∠A'EB'=180°,即可得到结论;
(3)分两种情况讨论:①当α+β≤90°时,②当α+β>90°时.
(1)如图:
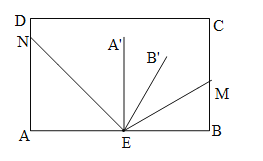
(2)由折叠的性质得:∠AEN=∠A'EN,∠BEM=∠B'EM.
∵2∠AEN+2∠BEM+∠A'EB'=180°,
∴∠A'EB'=180°-2(∠AEN+∠BEM)=180°-2(45°+30°)=30°;
(3)分两种情况讨论:
①当α+β≤90°时,如图1,由(2)可知:∠A'EB'=180°-2(∠AEN+∠BEM)=180°-2(α+β);
②当α+β>90°时,如图2,类似可得:∠A'EB'=2(∠AEN+∠BEM)-180°=2(α+β)-180°.
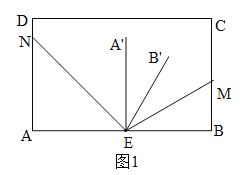
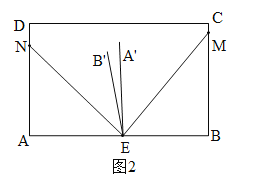
综上所述:∠A'EB'=180°-2(α+β)或2(α+β)-180°.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目