题目内容
在直角梯形ABCD中,AD⊥BC,AB⊥AD,AB=10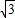 ,AD、BC的长是方程x2-20x+75=0的两根,那么,以点D为圆心、AD为半径的圆与以点C为圆心、BC为半径的圆位置关系是 .
,AD、BC的长是方程x2-20x+75=0的两根,那么,以点D为圆心、AD为半径的圆与以点C为圆心、BC为半径的圆位置关系是 .
【答案】分析:首先过点D作DE⊥BC于E,易证得四边形ABED是矩形,然后由勾股定理,求得CD的长,再根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.
解答: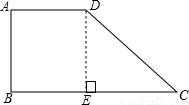 解:过点D作DE⊥BC于E,
解:过点D作DE⊥BC于E,
∵AD、BC的长是方程x2-20x+75=0的两根,
∴解得:x1=5,x2=15,如图所示:
可得:AD=5,BC=15,
∵AD∥BC,AB⊥BC,
∴AB∥DE,
∴四边形ABED是矩形,
∴DE=AB=10 ,BE=AD=5,∠DEC=90°,
,BE=AD=5,∠DEC=90°,
∴EC=BA-BE=15-5=10,
∴CD= =20,
=20,
∵AD+BC=20,
∴两圆的位置关系是外切.
故答案为:外切.
点评:此题考查了圆与圆的位置关系和梯形的性质矩形的判定与性质以及勾股定理的应用等知识.此题难度适中,解题的关键是注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.
解答:
 解:过点D作DE⊥BC于E,
解:过点D作DE⊥BC于E,∵AD、BC的长是方程x2-20x+75=0的两根,
∴解得:x1=5,x2=15,如图所示:
可得:AD=5,BC=15,
∵AD∥BC,AB⊥BC,
∴AB∥DE,
∴四边形ABED是矩形,
∴DE=AB=10
 ,BE=AD=5,∠DEC=90°,
,BE=AD=5,∠DEC=90°,∴EC=BA-BE=15-5=10,
∴CD=
 =20,
=20,∵AD+BC=20,
∴两圆的位置关系是外切.
故答案为:外切.
点评:此题考查了圆与圆的位置关系和梯形的性质矩形的判定与性质以及勾股定理的应用等知识.此题难度适中,解题的关键是注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.

练习册系列答案
相关题目
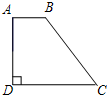 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
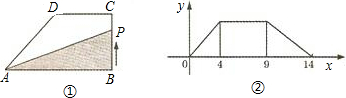
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )