题目内容
抛物线y=x2-4x-3与x轴交于点A，B，顶点为P，则△PAB的面积为
- A.
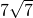
- B.
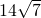
- C.
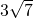
- D.12
A
分析：求出三点坐标，利用△PAB的面积=AB×P的纵坐标的绝对值÷2即可解答．
解答：令y=0，得抛物线y=x2-4x-3与x轴两交点坐标：A（2-
，0），B（2+，0），
∴AB=2，
又y=x2-4x-3=（x-2）2-7，
∴P（2，-7），△PAB的面积为
×2×7=7，
故选A．
点评：解决本题的关键是得到所求的量的等量关系，难点是确定△PAB的底和高．
分析：求出三点坐标，利用△PAB的面积=AB×P的纵坐标的绝对值÷2即可解答．
解答：令y=0，得抛物线y=x2-4x-3与x轴两交点坐标：A（2-
，0），B（2+，0），∴AB=2
，又y=x2-4x-3=（x-2）2-7，
∴P（2，-7），△PAB的面积为
×2×7=7，故选A．
点评：解决本题的关键是得到所求的量的等量关系，难点是确定△PAB的底和高．
练习册系列答案
阅读快车系列答案
相关题目
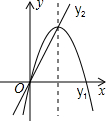如图，抛物线y1=-x2+4x和直线y2=2x．当y1＞y2时，x的取值范围是（ ）| A、0＜x＜2 | B、x＜0或x＞2 | C、x＜0或x＞4 | D、0＜x＜4 |