题目内容
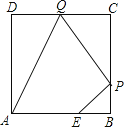
【题目】如图，矩形
的对角线相交于点
，
，
．
（1）求证：四边形
是菱形；
（2）若将题设中“矩形”这一条件改为“菱形”，其余条件不变，则四边形是__________形．
【答案】（1）证明见解析；（2）矩．
【解析】
（1）由PD∥AC，PC∥BD，易得四边形OCPD是平行四边形，又由矩形ABCD的对角线互相平分且相等，即可得OC=OD，继而证得四边形OCPD是菱形；
（2）由PD∥AC，PC∥BD，易得四边形OCPD是平行四边形，又由菱形的对角线互相垂直，即可得AC⊥BD，继而证得四边形OCPD是矩形．
（1）∵PD∥AC，PC∥BD，∴四边形OCPD是平行四边形．
∵四边形ABCD是矩形，∴AC=BD，OD
BD，OCAC，∴OC=OD，∴四边形OCPD是菱形；
（2）矩形．证明如下：
∵PD∥AC，PC∥BD，∴四边形OCPD是平行四边形．
∵四边形ABCD是菱形，∴AC⊥BD，∴∠COD=90°，∴四边形OCPD是矩形．
故答案为：矩．
练习册系列答案
相关题目
