题目内容
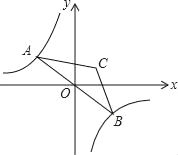
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.
【答案】3
【解析】分析:连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,证明△AOD∽△OCE,根据相似三角形的性质求出△AOD和△OCE面积比,根据反比例函数图象上点的特征求出S△AOD,得到S△EOC,求出k的值.
详解:连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,
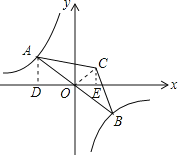
∵连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,
∴CO⊥AB,∠CAB=30°,
则∠AOD+∠COE=90°,
∵∠DAO+∠AOD=90°,
∴∠DAO=∠COE,
又∵∠ADO=∠CEO=90°,
∴△AOD∽△OCE,
∴![]() =tan60°=
=tan60°=![]() ,
,
∴![]() ,
,
∵点A是双曲线y=-![]() 在第二象限分支上的一个动点,
在第二象限分支上的一个动点,
∴S△AOD=![]() ×|xy|=
×|xy|=![]() ,
,
∴S△EOC=![]() ,即
,即![]() ×OE×CE=
×OE×CE=![]() ,
,
∴k=OE×CE=3,
故答案为:3.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】近期,我市持续出现雾霾天气,给广大市民的工作和生活造成了严重的影响.为此,“雾霾天气的主要成因”就成为了某校环保小组调查研究的课题,他们随机调查了部分市民,并对调查结果进行了整理,绘制了如图所示的不完整的统计图表.请根据图表中提供的信息解答下列问题:
级别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 |
|
B | 地面灰尘大,空气湿度低 |
|
C | 汽车尾部排放 |
|
D | 工厂造成污染 |
|
E | 其他 |
|
调查结果扇形统计图
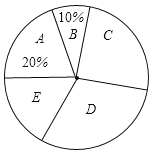
(1)填空:![]() ______,
______,![]() ______;
______;
(2)求出扇形统计图中E组所占的百分比以及扇形统计图中区域D所对应的扇形圆心角度数;