题目内容
如图,AB为⊙O直径,且弦CD⊥AB于,过点的切线与AD的延长线交于点.(1)若M是AD的中点,连接ME并延长ME交BC于N.求证:MN⊥BC.
(2)若cos∠C=
 ,DF=3,求⊙O的半径.
,DF=3,求⊙O的半径.(3)猜测线段AE、BE、CN、CB之间有怎样的数量关系?证明你的猜想.
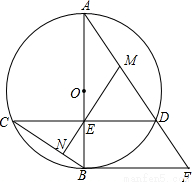
【答案】分析:(1)由弦CD⊥AB,M是AD的中点,得到EM为直角三角形AED斜边上的中线,则MA=ME,∠A=∠AEM,根据对顶角相等和同弧或等弧所对的圆周角相等得到∠AEM=∠BEN,∠ADE=∠EBN,则∠BEN+∠EBN=∠A+∠ADE=90°,则∠ENB=90°,即可得到结论;
(2)连BD,根据直径所对的圆周角为直角得到∠ADB=90°,根据切线的性质得到∠ABF=90°,利用相似三角形的判定易得Rt△FBD∽Rt△FAB,则FB:AF=DF:BF,即FB2=FD•FA,根据同弧或等弧所对的圆周角相等得∠A=∠C,则cos∠A= ,在Rt△ABF中,cos∠A=
,在Rt△ABF中,cos∠A=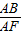 =
= ,不妨设AB=4x,则AF=5x,利用勾股定理可计算出BF=3x,则(3x)2=3•5x,解得x=
,不妨设AB=4x,则AF=5x,利用勾股定理可计算出BF=3x,则(3x)2=3•5x,解得x= ,易得到AB的长,即可得到⊙O的半径;
,易得到AB的长,即可得到⊙O的半径;
(3)由AB⊥CD,根据垂径定理得到CE=DE,易证得Rt△AED∽Rt△DEB,Rt△CEB∽Rt△CNE,则AE:DE=DE:BE,即DE2=AE•BE,CE:CN=CB:CE,即CE2=CN•CB,则可得AE•BE=CN•CB.
解答: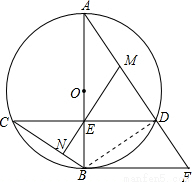 (1)证明:∵弦CD⊥AB,M是AD的中点,
(1)证明:∵弦CD⊥AB,M是AD的中点,
∴MA=ME,
∴∠A=∠AEM,
而∠AEM=∠BEN,∠ADE=∠EBN,
∴∠BEN+∠EBN=∠A+∠ADE=90°,
∴∠ENB=90°,
∴MN⊥BC;
(2)解:连BD,如图,
∵AB为直径,
∴∠ADB=90°,
又∵FB为⊙O的切线,
∴AB⊥BF,
∴∠ABF=90°,
∴Rt△FBD∽Rt△FAB,
∴FB:AF=DF:BF,即FB2=FD•FA,
∵∠A=∠C,cos∠C= ,
,
∴cos∠A= ,
,
在Rt△ABF中,cos∠A=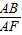 =
= ,不妨设AB=4x,则AF=5x,
,不妨设AB=4x,则AF=5x,
∴BF=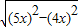 =3x,
=3x,
∴(3x)2=3•5x,解得x1= ,x2=0
,x2=0
∴x= ,
,
∴AB=4x=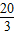 ,
,
∴⊙O的半径为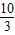 ;
;
(3)解:线段AE、BE、CN、CB之间的数量关系为AE•BE=CN•CB.理由如下:
∵AB⊥CD,
∴CE=DE,∠AED=90°,
而∠ADB=90°,
∴∠A=EDB,
∴Rt△AED∽Rt△DEB,
∴AE:DE=DE:BE,即DE2=AE•BE①,
又∵∠CEB=∠CNE=90°,
∴Rt△CEB∽Rt△CNE,
∴CE:CN=CB:CE,即CE2=CN•CB②,
由①②得AE•BE=CN•CB.
点评:本题考查了圆的综合题:垂直于弦的直径平分弦,并且平分弦所对的弧;圆的切线垂直于过切点的半径;在同圆或等圆中,同弧或等弧所对的圆周角相等,直径所对的圆周角为直角;运用相似三角形的判定与性质可得到线段的比例关系;运用勾股定理和三角函数进行几何计算.
(2)连BD,根据直径所对的圆周角为直角得到∠ADB=90°,根据切线的性质得到∠ABF=90°,利用相似三角形的判定易得Rt△FBD∽Rt△FAB,则FB:AF=DF:BF,即FB2=FD•FA,根据同弧或等弧所对的圆周角相等得∠A=∠C,则cos∠A=
 ,在Rt△ABF中,cos∠A=
,在Rt△ABF中,cos∠A=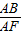 =
= ,不妨设AB=4x,则AF=5x,利用勾股定理可计算出BF=3x,则(3x)2=3•5x,解得x=
,不妨设AB=4x,则AF=5x,利用勾股定理可计算出BF=3x,则(3x)2=3•5x,解得x= ,易得到AB的长,即可得到⊙O的半径;
,易得到AB的长,即可得到⊙O的半径;(3)由AB⊥CD,根据垂径定理得到CE=DE,易证得Rt△AED∽Rt△DEB,Rt△CEB∽Rt△CNE,则AE:DE=DE:BE,即DE2=AE•BE,CE:CN=CB:CE,即CE2=CN•CB,则可得AE•BE=CN•CB.
解答:
 (1)证明:∵弦CD⊥AB,M是AD的中点,
(1)证明:∵弦CD⊥AB,M是AD的中点,∴MA=ME,
∴∠A=∠AEM,
而∠AEM=∠BEN,∠ADE=∠EBN,
∴∠BEN+∠EBN=∠A+∠ADE=90°,
∴∠ENB=90°,
∴MN⊥BC;
(2)解:连BD,如图,
∵AB为直径,
∴∠ADB=90°,
又∵FB为⊙O的切线,
∴AB⊥BF,
∴∠ABF=90°,
∴Rt△FBD∽Rt△FAB,
∴FB:AF=DF:BF,即FB2=FD•FA,
∵∠A=∠C,cos∠C=
 ,
,∴cos∠A=
 ,
,在Rt△ABF中,cos∠A=
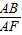 =
= ,不妨设AB=4x,则AF=5x,
,不妨设AB=4x,则AF=5x,∴BF=
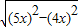 =3x,
=3x,∴(3x)2=3•5x,解得x1=
 ,x2=0
,x2=0∴x=
 ,
,∴AB=4x=
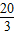 ,
,∴⊙O的半径为
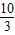 ;
;(3)解:线段AE、BE、CN、CB之间的数量关系为AE•BE=CN•CB.理由如下:
∵AB⊥CD,
∴CE=DE,∠AED=90°,
而∠ADB=90°,
∴∠A=EDB,
∴Rt△AED∽Rt△DEB,
∴AE:DE=DE:BE,即DE2=AE•BE①,
又∵∠CEB=∠CNE=90°,
∴Rt△CEB∽Rt△CNE,
∴CE:CN=CB:CE,即CE2=CN•CB②,
由①②得AE•BE=CN•CB.
点评:本题考查了圆的综合题:垂直于弦的直径平分弦,并且平分弦所对的弧;圆的切线垂直于过切点的半径;在同圆或等圆中,同弧或等弧所对的圆周角相等,直径所对的圆周角为直角;运用相似三角形的判定与性质可得到线段的比例关系;运用勾股定理和三角函数进行几何计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 6、如图,AB为直径,∠BED=40°,则∠ACD=( )
6、如图,AB为直径,∠BED=40°,则∠ACD=( ) 如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数. 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数. 如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为
如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为