ЬтФПФкШн
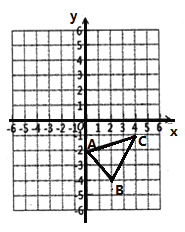
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌACЃНBCЃЌжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкЕуDЃЌBEЁЭMNгкЕуEЃЎ
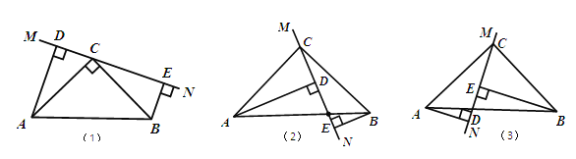
ЃЈ1ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМЃЈ1ЃЉЕФЮЛжУЪБЃЌЧѓжЄЃКDEЃНADЃЋBEЃЛ
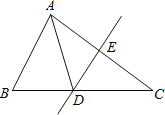
ЃЈ2ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМЃЈ2ЃЉЕФЮЛжУЪБЃЌЧѓжЄЃКDEЃНADЃBEЃЛ
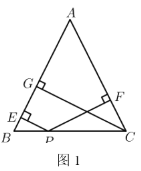
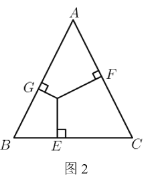
ЃЈ3ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМЃЈ3ЃЉЕФЮЛжУЪБЃЌЪдЮЪЃКDEЃЌADЃЌBEгадѕбљЕФЕШСПЙиЯЕЃПЧыаДГіетИіЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉDEЃНBEЃADЃЌжЄУїМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУДЙжБЕФЖЈвхЕУЁЯADC=ЁЯCEB=90ЁуЃЌдђИљОнЛЅгрЕУЁЯDAC+ЁЯACD=90ЁуЃЌдйИљОнЕШНЧЕФгрНЧЯрЕШЕУЕНЁЯDAC=ЁЯBCEЃЌШЛКѓИљОнЁАAASЁБПЩХаЖЯЁїADCЁеЁїCEBЃЌЫљвдCD=BEЃЌAD=CEЃЌдйРћгУЕШСПДњЛЛЕУЕНDE=AD+BEЃЛ
ЃЈ2ЃЉгыЃЈ1ЃЉжЄЗЈРрЫЦПЩжЄГіЁЯDAC=ЁЯBCEЃЌФмЭЦГіЁїADCЁеЁїCEBЃЌЕУЕНAD=CEЃЌCD=BEЃЌДгЖјгаDE=CE-CD=AD-BEЃЛ
ЃЈ3ЃЉгыЃЈ1ЃЉжЄЗЈРрЫЦПЩжЄГіЁЯDAC=ЁЯBCEЃЌФмЭЦГіЁїADCЁеЁїCEBЃЌЕУЕНAD=CEЃЌCD=BEЃЌгкЪЧгаDE=CD-CE=BE-ADЃЎ
ЃЈ1ЃЉжЄУїЃКЁпADЁЭMN,BEЁЭMN
ЁрЁЯADCЃНЁЯCEBЃН90Ёу
ЁрЁЯDACЃЋЁЯDCAЃН90Ёу
ЁпЁЯACBЃН90Ёу
ЁрЁЯECBЃЋЁЯDCAЃН90Ёу
ЁрЁЯDACЃНЁЯECB
дкЁїACDКЭЁїCBEжаЃЌ
Ёп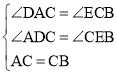
ЁрЁїACDЁеЁїCBE(AAS)
ЁрCEЃНAD, CDЃНBE
ЁпDEЃНCEЃЋCD
ЁрDEЃНADЃЋBE
ЃЈ2ЃЉжЄУїЃКгыЃЈ1ЃЉвЛбљПЩжЄУїЁїADCЁеЁїCEBЃЌ
ЁрCD=BEЃЌAD=CEЃЌ
ЁрDE=CE-CD=AD-BEЃЛ
ЃЈ3ЃЉDEЃНBEЃADЃЎжЄУїШчЯТЃК
жЄУїЃКжЄУїЃКЁпADЁЭMN,BEЁЭMN
ЁрЁЯADCЃНЁЯCEBЃН90Ёу
ЁрЁЯDACЃЋЁЯDCAЃН90Ёу
ЁпЁЯACBЃН90Ёу
ЁрЁЯECBЃЋЁЯDCAЃН90Ёу
ЁрЁЯDACЃНЁЯECB
дкЁїACDКЭЁїCBEжаЃЌ
Ёп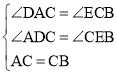
ЁрЁїACDЁеЁїCBE(AAS)
ЁрCEЃНAD, CDЃНBE
ЁрDE=CD-CE= BE-ADЃЛ

 ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИ
ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИ