题目内容
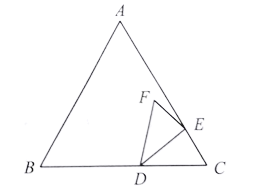
【题目】如图,等边三角形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,
上,![]() .点
.点![]() 为边
为边![]() 上一动点(不与点
上一动点(不与点![]() 重合),连接
重合),连接![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
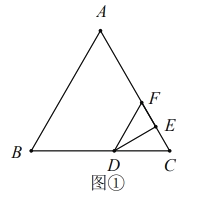
(1)当点![]() 在
在![]() 上时,求证:
上时,求证:![]() ;
;
(2)当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
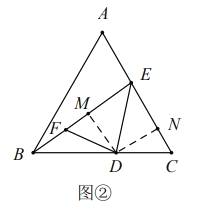
(3)连接![]() 设
设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 记
记![]()
![]() 是否存在最大值?若存在,请直接写出
是否存在最大值?若存在,请直接写出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)存在.
;(3)存在.![]() 最大值为
最大值为![]() .
.
【解析】
(1)根据轴对称图形性质,可得对称图形对应角等以及边等,结合等边三角形60°判断其同位角相等,进而推出两直线平行.
(2)根据轴对称图形性质,可得其对应边等以及对应角等,通过做垂直辅助线并结合等边三角形求解边长,根据“不同底但等高”面积原则求解边长比例,进而列方程求解.
(3)因为S1的面积确定,S面积的不确定性由S2决定,按照三角形面积公式将面积最值问题转化为线段最值问题,当S2的高最小时,其面积最小,S面积最大.
![]() 如图
如图![]() ,由轴对称性可知,
,由轴对称性可知,![]()
![]() ,
,
当点![]() 在
在![]() 上时,
上时,![]() ,
,
![]() .
.
![]() 由题意可知,
由题意可知,![]()
![]() ,
,
如图![]() ,过点
,过点![]() 作
作![]() ,垂足分别是点
,垂足分别是点![]() .
.
则![]() ,
,
设![]()
则![]() ,
,
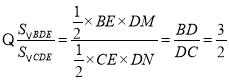 ,
,
![]() .
.
即![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 构建以
构建以![]() 为半径的圆弧,如下图所示,当
为半径的圆弧,如下图所示,当![]() 时,
时,![]() 到
到![]() 的距离最小,
的距离最小,![]() 取得最大值.
取得最大值.

![]() ,
,
![]() ,
,
∴![]() ,
,
所以存在最大值,![]() 最大值为
最大值为![]() .
.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】某校学生会干部对全校师生倡导的“武汉加油”的自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1∶5.
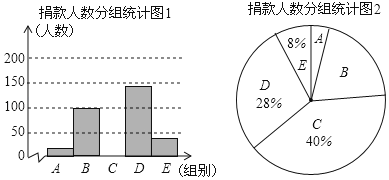
组别 | 捐款额x(元) | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | 40≤x<50 |
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”;
(3)根据统计情况,估计该校参加捐款的5000名学生有多少人捐款在20至50元之间.
【题目】2020蓉漂云招聘活动在4月25日正式启动,共发布了岗位13198个.某网络公司招聘一名高级网络工程师,应聘者小魏参加笔试和面试,成绩(100分制)如表所示:
笔试 | 面试 | |||||||
成绩 | 98 | 评委1 | 评委2 | 评委3 | 评委4 | 评委5 | 评委6 | 评委 7 |
94 | 95 | 92 | 99 | 98 | 97 | 96 | ||
其中规定:面试得分中去掉一个最高分和一个最低分,余下的面试得分的平均值作为应聘者的面试成绩.
(1)请计算小魏的面试成绩;
(2)如果面试成绩与笔试成绩按6:4的比例确定,请计算出小魏的最终成绩.
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
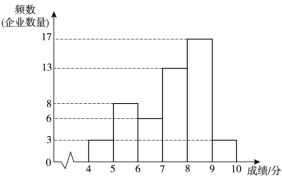
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.