题目内容
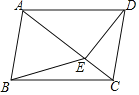
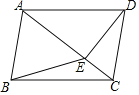
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若△ABE是等边三角形,四边形BCDE的面积等于2![]() ,求CE的长.
,求CE的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用两组对角相等的四边形是平行四边形进行证明;
(2)设CD的长为a,则CE=![]() a,,DE=
a,,DE=![]() a,S△CED=
a,S△CED=![]() a2,由面积关系可得
a2,由面积关系可得![]() a2+
a2+![]() a2=2
a2=2![]() ,可求a的值,即可求CE的长.
,可求a的值,即可求CE的长.
(1)证明:∵AB∥CD,
∴∠DAB+∠ADC=∠ABC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠DAB=∠BCD,且∠ABC=∠ADC,
∴四边形ABCD是平行四边形;
(2)∵△ABE是等边三角形,
∴AB=AE=CD,∠BAC=60°,
∵AB∥CD,
∴∠BAC=∠ACD=60°,
∵DE⊥AC,
∴∠DEC=90![]() ,
,
在Rt△CDE中,设CD的长为a,
则CE=![]() a,DE=
a,DE=![]() a,S△CED=
a,S△CED=![]() a2.
a2.
因为△CED与△CEB是同底等高的三角形,
∴S△CED=S△CEB,
又∵S四边形BCDE=S△CED+S△CEB=2![]() ,
,
∴![]() a2+
a2+![]() a2=2
a2=2![]() ,
,
∴a=2![]() ,
,
∴CE=![]() a=
a=![]() .
.

练习册系列答案
相关题目