题目内容
【题目】操作:将一把三角尺放在边长为1的正方形![]() 上,并使它的直角顶点
上,并使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() .
.
探究:设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
(1)点![]() 在
在![]() 边上时,线段
边上时,线段![]() 与线段
与线段![]() 之间有怎样的大小关系?试证明你观察得到的结论(如图1);
之间有怎样的大小关系?试证明你观察得到的结论(如图1);
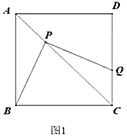
(2)点![]() 在边
在边![]() 上时设四边形
上时设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数解析式,并写出自变量的取值范围(如图2);
之间的函数解析式,并写出自变量的取值范围(如图2);
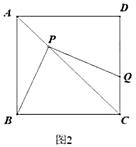
(3)点![]() 在线段
在线段![]() 上滑动时,
上滑动时,![]() 是否可能成为等腰三角形?如果可能,指出所有能使
是否可能成为等腰三角形?如果可能,指出所有能使![]() 成为等腰三角形的点
成为等腰三角形的点![]() 的位置,并直接写出相应的
的位置,并直接写出相应的![]() 的值;如果不可能,试说明理由(如图3).(图4、图5、图6的形状、大小相同,图4供操作、实验用,图5和图6备用).
的值;如果不可能,试说明理由(如图3).(图4、图5、图6的形状、大小相同,图4供操作、实验用,图5和图6备用).
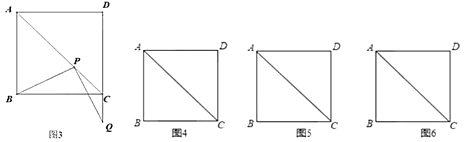
【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() (
(![]() );(3)
);(3)![]() 可能成为等腰三角形,Q与点D重合时,x=0;Q在边DC的延长线上时,x=1
可能成为等腰三角形,Q与点D重合时,x=0;Q在边DC的延长线上时,x=1
【解析】
(1)过点P作![]() ,分别交AB于点M,交CD于点N,则四边形AMND和四边形BCNM都是矩形,
,分别交AB于点M,交CD于点N,则四边形AMND和四边形BCNM都是矩形,![]() 和
和![]() 都是等腰三角形,然后利用等腰三角形的性质和等量代换证明
都是等腰三角形,然后利用等腰三角形的性质和等量代换证明![]() ,从而可证
,从而可证![]() ;
;
(2)设![]() ,然后分别表示出BM,CQ,PN的长度,然后利用
,然后分别表示出BM,CQ,PN的长度,然后利用![]() 和
和![]() 求出各自的面积 ,最后利用
求出各自的面积 ,最后利用![]() 即可求解;
即可求解;
(3)分三种情况:点Q与点D重合;当点Q在边DC的延长线上;Q与点C重合,分别进行讨论即可得出答案.
(1)![]() ,理由如下:
,理由如下:
过点P作![]() ,分别交AB于点M,交CD于点N,则四边形AMND和四边形BCNM都是矩形,
,分别交AB于点M,交CD于点N,则四边形AMND和四边形BCNM都是矩形,

∵四边形ABCD是正方形,
∴![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
∴![]() .
.
![]() ,
,
![]() .
.
又∵![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ;
;
(2)由(1)知![]() ,则
,则![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
即![]() (
(![]() );
);
(3)![]() 可能成为等腰三角形,理由如下:
可能成为等腰三角形,理由如下:
①当点P与点A重合,点Q与点D重合,这时![]() ,
,![]() 是等腰三角形,此时
是等腰三角形,此时![]() ;
;
②当点Q在边DC的延长线上,且![]() 时,
时,![]() 是等腰三角形,如图,
是等腰三角形,如图,
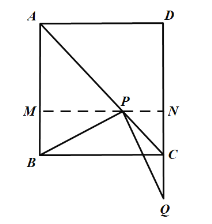
此时![]() ,
,
![]() ,
,
当![]() 时,解得
时,解得![]() ;
;
③![]() ,Q与点C重合,
,Q与点C重合,![]() ,
, ![]() 不存在;
不存在;
综上所述,当![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

 考前必练系列答案
考前必练系列答案