题目内容
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx(m≠0)与x轴交于A,B两点(点A在点B的左侧).
(1)求点A,B的坐标及抛物线的对称轴;
(2)过点B的直线l与y轴交于点C,且tan∠ACB=2,直接写出直线l的表达式;
(3)如果点P(x1 , n)和点Q(x2 , n)在函数y=mx2﹣4mx(m≠0)的图象上,PQ=2a且x1>x2 , 求x12+ax2﹣6a+2的值.
【答案】
(1)解:当y=mx2﹣4mx=mx(x﹣4)=0时,x1=0,x2=4,
∵点A在点B的左侧,
∴A点坐标为(0,0),B点坐标为(4,0).
抛物线对称轴为直线:x=﹣ ![]() =2
=2
(2)解:设直线l的表达式为y=kx+b(k≠0).
当点C在y轴正半轴时,点C的坐标为(0,2),

将B(4,0)、C(0,2)代入y=kx+b中,
![]() ,解得:
,解得: 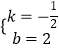 ,
,
此时直线l的表达式为y=﹣ ![]() x+2;
x+2;
当点C在y轴负半轴时,点C的坐标为(0,﹣2),
将B(4,0)、C(0,﹣2)代入y=kx+b中,
![]() ,解得:
,解得: 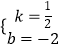 ,
,
此时直线l的表达式为y= ![]() x﹣2.
x﹣2.
综上所述:直线l的表达式为y=﹣ ![]() x+2或y=
x+2或y= ![]() x﹣2
x﹣2
(3)解:∵点P(x1,n)和点Q(x2,n)在函数y=mx2﹣4mx(m≠0)的图象上,
∴点P与点Q关于对称轴x=2对称.
∵PQ=2a,x1>x2,
∴x1=2+a,x2=2﹣a,
∴x12+ax2﹣6a+2=(2+a)2+a(2﹣a)﹣6a+2=6.
【解析】(1)把y=0代入抛物线的解析式,解一元二次方程即可求出x的值,由点A在点B的左侧,从而得出A、A两点的坐标;(2)此题分两种情况:点C在在y轴负半轴时与点C在在y轴正半轴时,设直线l的表达式为y=kx+b(k≠0),由tan∠ACB=2得出C点的坐标,将B、C两点的坐标分别代入y=kx+b得出方程组,解方程组得出k,b的值即可;(3)由P、Q两点的纵坐标及都在抛物线上知点P与点Q关于对称轴x=2对称,由PQ=2a,x1>x2,得x1=2+a,x2=2﹣a,代入x12+ax2﹣6a+2即可。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案