题目内容
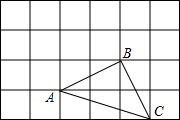
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.
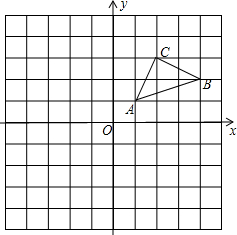
(1)建立如图所示的直角坐标系,请在图中标出△ABC的外接圆的圆心P的位置,并填写:
①圆心P的坐标:P(______,______);
②⊙P的半径为______.
(2)将△ABC绕点A逆时针旋转90度得到△ADE,画出图形,并求线段BC扫过的图形的面积.

(1)建立如图所示的直角坐标系,请在图中标出△ABC的外接圆的圆心P的位置,并填写:
①圆心P的坐标:P(______,______);
②⊙P的半径为______.
(2)将△ABC绕点A逆时针旋转90度得到△ADE,画出图形,并求线段BC扫过的图形的面积.

(1)如图所示:①圆心P的坐标:P(5,3);
②⊙P的半径为:
=2
,
故答案为:(5,3),2
;
(2)∵由勾股定理得:AC=2
,AB=2
,
∵将△ABC绕点A逆时针旋转90°得到△ADE,
∴线段BC扫过的图形的面积=S扇形ACE+S△ABC-S扇形ABD-S△ADE
=
+
×4×2-
-
×4×2
=8π.


②⊙P的半径为:
| 42+22 |
| 5 |
故答案为:(5,3),2
| 5 |
(2)∵由勾股定理得:AC=2
| 10 |
| 2 |
∵将△ABC绕点A逆时针旋转90°得到△ADE,
∴线段BC扫过的图形的面积=S扇形ACE+S△ABC-S扇形ABD-S△ADE
=
90π×(2
| ||
| 360 |
| 1 |
| 2 |
90π×(2
| ||
| 360 |
| 1 |
| 2 |
=8π.



练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 斜边DE交AC边于点F,则图中△CDF的面积为______.
斜边DE交AC边于点F,则图中△CDF的面积为______.