题目内容
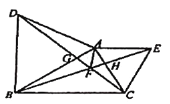
【题目】如图,以![]() 的边
的边![]() 为边,向外作等边
为边,向外作等边![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)请直接写出![]() 的度数.
的度数.
【答案】(1)证明见解析;(2) 120![]() ;(3) 60
;(3) 60![]()
【解析】
(1)由三角形ABD与三角形ACE都为等边三角形,利用等边三角形的性质得到两组对应边相等,两三角形的内角都为60°,利用等式的性质得到∠DAC=∠BAE,利用SAS可得出△DAC≌△BAE,得证;
(2)由△DAC≌△BAE,利用全等三角形的对应角相等得到∠ACD=∠AEB,而∠DFE为三角形EFC的外角,利用外角的性质列出关系式,等量代换后即可求出其度数.
(3)作AM⊥BE,AN⊥DC,利用全等三角形及面积法证得AM=AN,点A在∠DFE的平分线上,从而求得结论.
(1)∵△ABD和△ACE都为等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=∠AEC=∠ACE=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,
在△DAC和△BAE中,
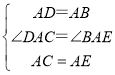
∴△DAC≌△BAE(SAS)
∴![]() ;
;
(2)由(1)中△DAC≌△BAE得:![]()
∵∠DFE为三角形EFC的外角,
∴∠DFE=∠FCE+∠CEF=∠FCA+∠ACE+∠CEF=∠ACE+∠CEF+∠FEA=∠ACE+∠AEC=60![]() =120
=120![]() ;
;
(3)过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.
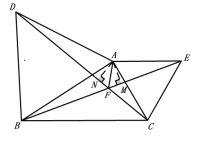
∵由(1)知:△DAC≌△BAE,
∴![]() =
=![]() ,
,![]()
∴![]() DCAN=
DCAN=![]() BEAM
BEAM
∴AM=AN
∴点A在∠DFE的平分线上,
即FA平分∠DFE
∴∠AFD=![]() ∠DFE=60
∠DFE=60![]() .
.

【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n=400时,绿豆发芽的频率为0.955,所以绿豆发芽的概率是0.955;
②根据上表,估计绿豆发芽的概率是0.95;
③若n为4000,估计绿豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ① B. ①② C. ①③ D. ②③