题目内容
如图,四边形ABCD是矩形,F是AD上一点,E是CB延长线上一点,且四边形AECF是等腰梯形,下列结论中不一定正确的是( )
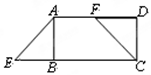

| A.AE=FC | B.AD=BC | C.BE=AF | D.∠E=∠CFD |
D.
试题分析:已知四边形AECF是等腰梯形可得AE=FC.又因为四边形ABCD是矩形可得AD=BC,∠AEB=CFD.
解答:解:已知四边形AECF是等腰梯形,可得AE=FC;
又∵四边形ABCD的矩形,可得AD=BC;
∵AB=CD,AE=FC,∠ABC=∠CDF,
∴△AEB≌△CFD,
∴∠AEB=∠CFD.
所以D不正确,
故选D.
考点: 1.等腰梯形的性质;2.矩形的性质.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
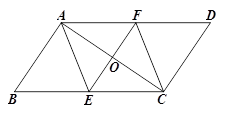


 =____________.
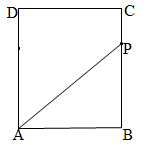
=____________.
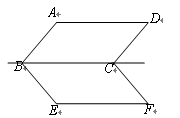
 ∥
∥ ∥
∥ ∥
∥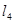 ,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为 .
,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为 .