Question

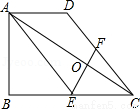
如图，已知△ABC中，∠B=90°，BC=3，AB=4，D是边AB上一点，DE∥BC交AC于点E，将△ADE沿DE翻折得到△A′DE，若△A′EC是直角三角形，则AD长为　

 

 

Answer 1

．

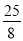【解析】

试题分析：先根据勾股定理得到AC=5，再根据平行线分线段成比例得到AD：AE=AB：AC=4：5，设AD=x，则AE=A′E=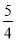x，EC=5-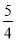x，A′B=2x-4，在Rt△A′BC中，根据勾股定理得到A′C，再根据△A′EC是直角三角形，根据勾股定理得到关于x的方程，解方程即可求解．

试题解析：在△ABC中，∠B=90°，BC=3，AB=4，

∴AC=5，

∵DE∥BC，

∴AD：AB=AE：AC，即AD：AE=AB：AC=4：5，

设AD=x，则AE=A′E=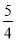x，EC=5-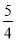x，A′B=2x-4，

在Rt△A′BC中，A′C=，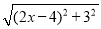

∵△A′EC是直角三角形，

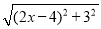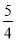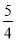∴（）2+（5-x）2=（x）2，

解得x1=4（不合题意舍去），x2=．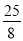

故AD长为．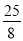

考点：翻折变换（折叠问题）．