Question

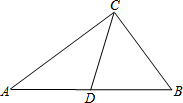
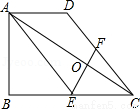
已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，BC=2AD，点E是BC的中点、F是CD上的点，联结AE、EF、AC．

（1）求证：AO•OF=OC•OE；

（2）若点F是DC的中点，联结BD交AE于点G，求证：四边形EFDG是菱形．

 

 

Answer 1

(1)证明见解析；（2）证明见解析.

【解析】

试题分析：（1）由BC=2AD，点E是BC的中点，可得AD=CE，又由AD∥BC，可得四边形AECD是平行四边形，即可得AE∥CD，继而证得△AOE∽△COF，即可判定AO•OF=OC•OE；

（2）易得EF是△BCD的中位线，则可判定四边形EFDG是平行四边形，又由直角三角形斜边上的中线的性质，证得DG=EG，继而证得四边形EFDG是菱形．

试题解析：（1）∵BC=2AD，点E是BC的中点，

∴AD=E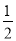C=BC，

∵在梯形ABCD中，AD∥BC，

∴四边形AECD是平行四边形，

∴AE∥CD，

∴△AOE∽△COF，

∴OA：OC=OE：OF，

∴AO•OF=OC•OE；

（2）∵E是BC的中点，F是CD的中点，

∴EF是△BCD的中位线，

∴EF∥BD，

∵AE∥CD，

∴四边形EFDG是平行四边形，

∵AD∥BC，

∴△ADG∽△EBG，

∴DG：BG=AD：EB=AG：EG，

∵AD=BE=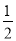BC，

∴AG=EG，DG=BG，

∵∠ABC=90°，

∴BG=G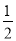E=AE，

∴EG=DG，

∴四边形EFDG是菱形．

考点：1.相似三角形的判定与性质；2.菱形的判定；3.梯形．