Question

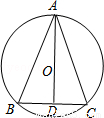
如图，已知AD既是△ABC的中线，又是角平分线，请判断：

（1）△ABC的形状；

（2）AD是否过△ABC外接圆的圆心O，⊙O是否是△ABC的外接圆，并证明你的结论．

 

 

Answer 1

证明见解析.

【解析】

试题分析：（1）过点D作DE⊥AB于点E，DF⊥AC于点F，根据HL定理可得出△BDE≌△CDF，进而得出结论；

（2）根据等腰三角形三线合一的性质可知AD⊥BC，再由BD=CD，可知AD过圆心O，故可得出结论．

试题解析：（1）答：△ABC是等腰三角形．

证明：过点D作DE⊥AB于点E，DF⊥AC于点F．

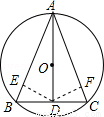
∵AD是角平分线，

∴DE=DF．

又∵AD是△ABC的中线，

∴BD=CD，

在Rt△BDE与Rt△CDF中，

，

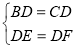∴△BDE≌△CDF（HL）．

∴∠B=∠C，

∴AB=AC，即△ABC是等腰三角形；

（2）答：AD过△ABC的外接圆圆心O，⊙O是△ABC的外接圆．

证明：∵AB=AC，AD是角平分线，

∴AD⊥BC，

又∵BD=CD，

∴AD过圆心O．

作边AB的中垂线交AD于点O，交AB于点M，则点O就是△ABC的外接圆圆心，

∴⊙O是△ABC的外接圆．

考点：1.三角形的外接圆与外心；2.全等三角形的判定与性质．