Question

【题目】已知抛物线经过点和．下列结论：

①；

②；

③当时，抛物线与轴必有一个交点在点的右侧；

④抛物线的对称轴为．

其中结论正确的个数有（ ）

A.4个B.3个C.2个D.1个

Answer 1

【答案】A

【解析】

由抛物线y＝ax2＋bx＋c（a≠0）经过点（1，0），得到ab＋c＝0，抛物线y＝ax2＋bx＋c（a≠0）经过点（1，1），于是得到a＋b＋c＝1，由于ab＋c＝0，得到，b＝，故可判断①；推出b24ac＝4a（a）＝2a＋4a2＝（2a）2≥0，故可判断②；当a＜0时，由b24ac＝（2a）2＞0，得到抛物线y＝ax2＋bx＋c与x轴有两个交点，设另一个交点的横坐标为x，根据根与系数的关系得到x＝1＞1，即抛物线与x轴必有一个交点在点（1，0）的右侧，故可判断③正确；④抛物线的对称轴公式即可得到x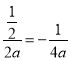＝＝，故可判断④正确．

①由抛物线y＝ax2＋bx＋c（a≠0）经过点（1，0），得到ab＋c＝0，

抛物线y＝ax2＋bx＋c（a≠0）经过点（1，1），

∴a＋b＋c＝1，又ab＋c＝0，

两式相加，得2（a＋c）＝1，，

两式相减，得2b＝1，b＝．故①正确；

∵b24ac＝4a（a）＝2a＋4a2＝（2a）2≥0，

当2a＝0，即a＝时，b24ac＝0，故②正确；

③当a＜0时，∵b24ac＝（2a）2＞0，

∴抛物线y＝ax2＋bx＋c与x轴有两个交点，设另一个交点的横坐标为x，

则1x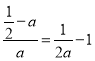＝＝，即x＝1，

∵a＜0，∴＞0，

∴x＝1＞1，

即抛物线与x轴必有一个交点在点（1，0）的右侧，故③正确；

④抛物线的对称轴为x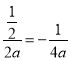＝＝，故④正确．

故选A．