题目内容
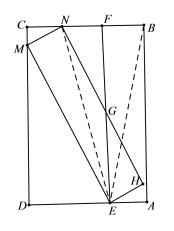
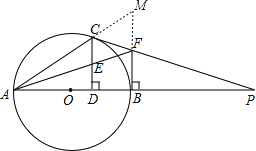
【题目】如图,已知AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C,CD⊥AB于点D,过B点作AP的垂线交PC于点F.
(1)求证:E是CD的中点;
(2)若FB=FE=2,求⊙O的半径.

【答案】(1)证明见解析;(2)2![]() .
.
【解析】
(1)延长BF、AC交于点M,则结合切线可得BF=FM,再结合平行线分线段成比例可求得CE=DE;
(2)结合条件可证得PF=AF,在Rt△PFB中,可得到PF和PB的关系,再结合PC是切线利用切割线定理可得到PB和PF的关系,可求得PB的长,则可求得AO的长,即⊙O的半径.
(1)证明:如图,延长BF、AC交于点M,
∵BF⊥AB,∴FB是⊙O的切线,
又CF是⊙O的切线,
∴CF=BF,
∴∠FCB=∠FBC,
又AB为直径,
∴∠BCM=90°,
∴∠CBM+∠M=∠BCF+∠FCM=90°,
∴∠FCM=∠M,
∴CF=MF,
∴BF=MF,
∵CD∥MB,
∴![]() ,
,
∴CE=ED,
即E是CD的中点;
(2)解:
∵BF=EF=2=FC=FM,
∴∠FCE=∠FEC=∠AED,
又CD⊥AB,
∴∠FAB+∠AED=∠ECF+∠P,
∴∠FAB=∠P,
∴AF=PF,
∴AB=PB,
设AB=PB=x,PF=y,
则在Rt△PBF中,由勾股定理可得y2=22+x2①,
又由切割线定理可得(y+2)2=x2x=2x2②,
则可解得x=4![]() ,y=6,
,y=6,
∴AO=![]() AB=2
AB=2![]() .
.

【题目】近视镜镜片的焦距![]() (单位:米)是镜片的度数
(单位:米)是镜片的度数![]() (单位:度)的函数,下表记录了一组数据:
(单位:度)的函数,下表记录了一组数据:
| … | 100 | 250 | 400 | 500 | … |
| … | 1.00 | 0.40 | 0.25 | 0.20 | … |
(1)在下列函数中,符合上述表格中所给数据的是_________;
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)利用(1)中的结论计算:当镜片的度数为200度时,镜片的焦距约为________米.
【题目】科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ | … | ﹣5 | ﹣3 | 2 | … |
植物高度增长量h/mm | … | 34 | 46 | 41 | … |
科学家推测出h(mm)与t之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为( )
A. ﹣2℃ B. ﹣1℃ C. 0℃ D. 1℃