Question

【题目】如图，在△ABC中，AB＝CB，∠ABC＝90°，D为AB延长线上一点，点E在BC边上，且BE＝BD，连结AE、DE、DC．

① 求证：△ABE≌△CBD；

② 若∠CAE＝30°，求∠BDC的度数．

Answer 1

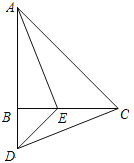
【答案】①证明见解析②∠BDC＝75°

【解析】试题分析：（1）利用“边角边”证明△ABE≌△CBD即可；②先根据等腰直角三角形的锐角都是45°求出∠CAB，再求出∠BAE，然后根据全等三角形对应角相等求出∠BCD，再根据直角三角形两锐角互余其解即可；

试题解析：

（1）证明：∵∠ABC=90°，D为AB延长线上一点，

∴∠ABE=∠CBD=90°，

在△ABE和△CBD中，

，

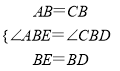∴△ABE≌△CBD（SAS）；

（2）∵AB=CB，∠ABC=90°，

∴∠CAB=45°，

∵∠CAE=30°，

∴∠BAE=∠CAB-∠CAE=45°-30°=15°，

∵△ABE≌△CBD，

∴∠BCD=∠BAE=15°，

∴∠BDC=90°-∠BCD=90°-15°=75°；