题目内容
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连结OB,将纸片OABC沿OB折叠,使点A落在点Aˊ的位置上,若OA=1,∠OBA=30°,则点Aˊ的坐标为
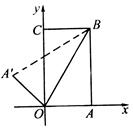


过A′作A′D⊥x轴与点D.
在直角△OAB中,∠OBA=30°∴∠BOA=60°
∴∠A′OB=∠BOA=60°
∴∠A′OD=60°
在直角△A′OD中,OD=OA′•cos60°=1× =
= ;
;
A′D=A′O•sin60°=1×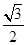 =
=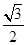 .
.
∴点A'的坐标为(- ,
, 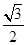 ).
).

在直角△OAB中,∠OBA=30°∴∠BOA=60°
∴∠A′OB=∠BOA=60°
∴∠A′OD=60°
在直角△A′OD中,OD=OA′•cos60°=1×
 =
= ;
;A′D=A′O•sin60°=1×
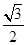 =
=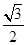 .
.∴点A'的坐标为(-
 ,
, 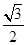 ).
).
练习册系列答案
相关题目



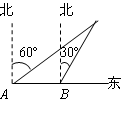
 ,AB=8cm,AC=4cm,则△ABC的面积= cm2.
,AB=8cm,AC=4cm,则△ABC的面积= cm2.

