题目内容
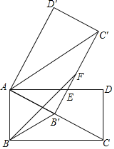
【题目】如图,在矩形![]() 中,把点
中,把点![]() 沿
沿![]() 对折,使点
对折,使点![]() 落在
落在![]() 上的
上的![]() 点,已知
点,已知![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点,我们把这条直线称为抛物线的切线,已知抛物线经过点![]() ,
,![]() ,且直线
,且直线![]() 是该抛物线的切线,求抛物线的解析式;
是该抛物线的切线,求抛物线的解析式;
(3)已知直线![]() 与(2)中的抛物线交于
与(2)中的抛物线交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .求证:
.求证:![]() 为定值.(参考公式:在平面直角坐标系中,已知点
为定值.(参考公式:在平面直角坐标系中,已知点![]() ,
,![]() ,则
,则![]() ,
,![]() 两点之间的距离为
两点之间的距离为![]() )
)

【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
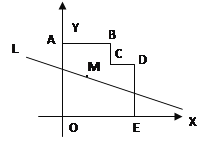
(1)根据矩形的性质可得∠AOC=90°,然后由折叠的性质可知AF=AD=10,根据勾股定理求出OF的长,即可求出点F的坐标;
(2)根据抛物线过点O和点F,设抛物线的解析式为![]() ,然后联立直线
,然后联立直线![]() ,根据该直线与抛物线仅有一个交点,令△=0即可求出a的值,从而求出结论;
,根据该直线与抛物线仅有一个交点,令△=0即可求出a的值,从而求出结论;
(3)联立方程组,设![]() ,
,![]() ,
,![]() ,根据根与系数的关系可得则
,根据根与系数的关系可得则![]() ,
,![]() ,再根据平面直角坐标系中任意两点之间的距离公式代入并化简即可.
,再根据平面直角坐标系中任意两点之间的距离公式代入并化简即可.
解:(1)∵四边形AOCD为矩形
∴∠AOC=90°
由折叠的性质可知AF=AD=10,
在Rt△OAF中,OF=![]()
∴![]() .
.
(2)根据题意,设抛物线的解析式为![]() ,联立直线
,联立直线![]() 得:
得:![]() .
.
则由![]() 得
得![]() .
.
故抛物线的方程为![]() .
.
(3)由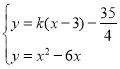 得
得![]() .
.
所以设![]() ,
,![]() ,
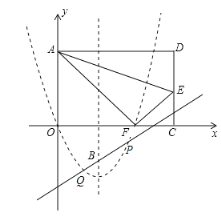
,![]() ,如下图所示
,如下图所示
则![]() ,
,![]()
而![]() ,
,![]() .
.
从而,![]()
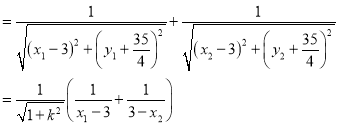

即![]() 为定值4.
为定值4.

【题目】某校为了解九年级学生的物理实验操作情况,进行了抽样调查.随机抽取了40名同学进行实验操作,成绩如下:
21 | 22 | 22 | 23 | 23 | 23 | 23 | 22 | 24 | 24 |
25 | 23 | 21 | 25 | 24 | 25 | 23 | 22 | 24 | 25 |
23 | 23 | 24 | 24 | 24 | 24 | 23 | 25 | 25 | 21 |
21 | 23 | 23 | 24 | 25 | 24 | 22 | 24 | 22 | 24 |
整理上面数据,得到如下统计图:

样本数据的平均数、众数、中位数如表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | m | 24 | 23 |
根据以上信息,解答下列问题:
(1)如表中平均数![]() 的值为_______;
的值为_______;
(2)扇形统计图中“ 24分”部分的圆心角大小为_______度;
(3)根据样本数据,请估计该校九年级320名学生中物理实验操作得满分的学生人数.