题目内容
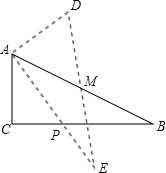
【题目】已知：如图，Rt△ABC中，∠C＝90°，∠BAC＝30°，延长CA至D点，使AD＝AB．求：
(1)求∠D及∠DBC；
(2)求tanD及tan∠DBC；
(3)请用类似的方法，求tan22.5°．
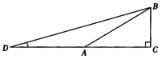
【答案】（1）∠D=15°，∠DBC=75°；（2）
；
（3）
【解析】
（1）利用外角性质得∠D=15°,∠DBC=75°；（2）设BC=1,根据30°角所对直角边等于斜边一半表示出直角边,利用正切值定义即可解题；（3）作出图形,根据外角性质和等腰直角三角形性质即可解题,见详解.
解：(1) ∵AD=AB
∴ ∠D+∠DBA=30°（外角性质）
∴∠D＝15°，∠DBC＝15°+60°=75°；
(2)设BC=1 则AB=AD=2,（30°角所对直角边等于斜边一半）
∴AC=
（勾股定理）
∴
,
(3)见下图, Rt△ABC中，∠C＝90°，∠BAC＝45°，延长CA至D点，使AD＝AB．
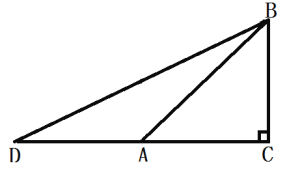
∴ ∠D+∠DBA=45°（外角性质）
∴∠D＝22.5°，
设BC=1,
∴AC=1,AB=
,
∴
练习册系列答案
阅读快车系列答案
相关题目
