题目内容
【题目】如图,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论:①△BDF、△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.正确的是( )

A. ③④ B. ①②③ C. ①② D. ②③④
【答案】B
【解析】由平行线得到角相等,由角平分线得角相等,根据平行线的性质及等腰三角形的判定和性质.
解答:解:∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∵BF是∠ABC的平分线,CF是∠ACB的平分线,
∴∠FBC=∠DFB,∠FCE=∠FCB,
∵∠DBF=∠DFB,∠EFC=∠ECF,
∴△DFB,△FEC都是等腰三角形.
∴DF=DB,FE=EC,即有DE=DF+FE=DB+EC,
∴△ADE的周长AD+AE+DE=AD+AE+DB+EC=AB+AC.
故选C.

练习册系列答案
相关题目
【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
组别 | 分组 | 频数 | 频率 |
1 | 50≤x<60 | 9 | 0.18 |
2 | 60≤x<70 | a | |
3 | 70≤x<80 | 20 | 0.40 |
4 | 80≤x<90 | 0.08 | |
5 | 90≤x≤100 | 2 | b |
合计 |
请根据以上频率分布表和频率分布直方图,回答下列问题: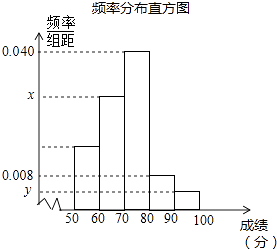
(1)求出a、b、x、y的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内?
(3)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)