题目内容
在ΔABC中,D为BC的中点,E为AC上的任意一点,BE交AD于点O.某学生在研究这一问题时,发现了如下事实: 如图1,当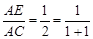 时,有
时,有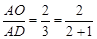 ;
;
如图2,当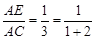 时,有
时,有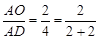 ;
;
如图3,当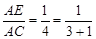 时,有
时,有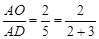 ;在图4中,当
;在图4中,当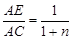 时,
时,
参照上述研究的结论,请你猜想用n表示AO∶AD的一般结论,并给出证明.
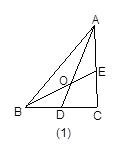
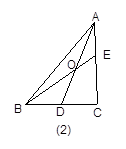
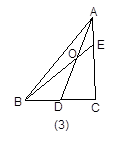
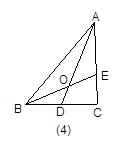
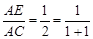 时,有
时,有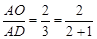 ;
;如图2,当
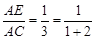 时,有
时,有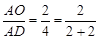 ;
;如图3,当
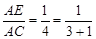 时,有
时,有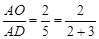 ;在图4中,当
;在图4中,当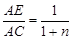 时,
时,参照上述研究的结论,请你猜想用n表示AO∶AD的一般结论,并给出证明.
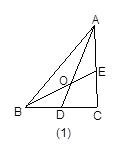
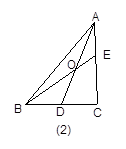
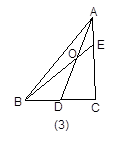
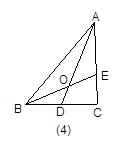
结论: AE∶AC=1∶(1+n)时,
AO∶AD=2∶(2+n).
证明:如图4,作DF∥BE,交AC于F.
∵BD=DC,∴EF=FC.
∵AE∶AC=1∶(1+n),∴AE∶EC=1∶n=2∶2n.
∴AE∶EF=2∶n.
∴AO∶AD=AE∶EF=2∶(2+n).
AO∶AD=2∶(2+n).
证明:如图4,作DF∥BE,交AC于F.
∵BD=DC,∴EF=FC.
∵AE∶AC=1∶(1+n),∴AE∶EC=1∶n=2∶2n.
∴AE∶EF=2∶n.
∴AO∶AD=AE∶EF=2∶(2+n).
过D作DF∥BE,即求AE:AD,因为 AE∶AC=1∶(1+n),可以根据平行线分线段成比例,及线段相互间的关系即可得出.

练习册系列答案
相关题目
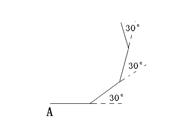
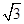 的山坡向上走了600m,则他升高了( )
的山坡向上走了600m,则他升高了( )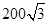 m
m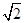 m
m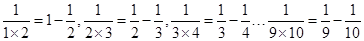

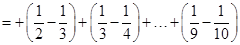
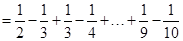

 ; ②
; ② 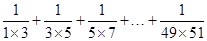
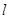 ,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸
,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸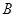 点到公路的距离,请你设计一个测量方案.要求:
点到公路的距离,请你设计一个测量方案.要求:
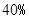 ,
,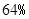 .已知第一季度男女皮鞋的销售总收入为200万元.
.已知第一季度男女皮鞋的销售总收入为200万元.