题目内容
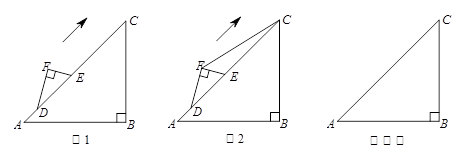
将等腰Rt△ABC和等腰Rt△ADE按图1方式放置,∠A=90°, AD边与AB边重合, AB=2AD=4.将△ADE绕点A逆时针方向旋转一个角度α(0°≤α≤180°),BD的延长线交直线CE于点P.
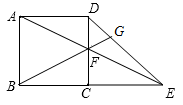
(1)如图2,BD与CE的数量关系是 , 位置关系是 ;
(2)在旋转的过程中,当AD⊥BD时,求出CP的长;
(3)在此旋转过程中,求点P运动的路线长.[
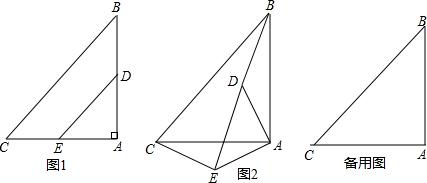
(1)如图2,BD与CE的数量关系是 , 位置关系是 ;
(2)在旋转的过程中,当AD⊥BD时,求出CP的长;
(3)在此旋转过程中,求点P运动的路线长.[

(1)BD=EC,BD⊥CE;(2) ;(3)
;(3) .
.
 ;(3)
;(3) .
.试题分析:(1)利用三角形中位线性质以及等腰直角三角形的性质得出即可.
(2)首先得出△ABD≌△ACE(SAS),进而求出四边形ADPE为正方形,即可得出CP的长.
(3)由(2)知,当α=60°时,∠PBA最大,且∠PBA=30°,此时∠AOP=60°,得出点P运动的路线是以O为圆心,OA长为半径的弧长
 ,进而利用弧长公式求出即可.
,进而利用弧长公式求出即可.试题解析:(1)BD=EC,BD⊥CE.理由如下:
∵等腰Rt△ABC和等腰Rt△ADE按图1方式放置,∠A=90°, AD边与AB边重合, AB=2AD=4,
∴D,E分别是AB和AC的中点.
∴BD=EC=AD=AE,BD⊥CE.
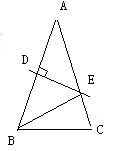
(2)如图3所示:
∵△ABC和△ADE都是等腰三角形,∴AB=AC,AD=AE.
∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE.
在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).∴∠ABD=∠ACE.
∵∠1=∠2,∴BP⊥CE.
∵AD⊥BP,∠DAE=90°,AD=AE,∴四边形ADPE为正方形.∴AD=PE=2.
∵∠ADB=90°,AD=2,AB=4,∴∠ABD=30°.
∴BD=CE=
 .
.∴CP=CE-PE=
 .
.
(3)如图4,取BC的中点O,连接OP、OA,
∵∠BPC=∠BAC=90°,∴OP=OA=
 BC=
BC= .
.在此旋转过程中(0°≤α≤180°),由(2)知,当α=60°时,∠PBA最大,且∠PBA=30°,此时∠AOP=60°,
∴点P运动的路线是以O为圆心,OA长为半径的弧长
 .
.∴点P运动的路线长为:


练习册系列答案
相关题目
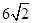 ,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).