题目内容
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(0,2)和B(1,
经过点A(0,2)和B(1,![]() ).
).
(1)求该抛物线的表达式;
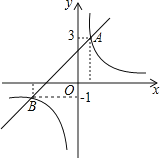
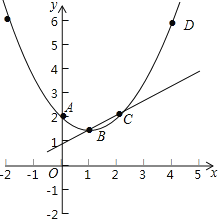
(2)已知点C与点A关于此抛物线的对称轴对称,点D在抛物线上,且点D的横坐标为4,求点C与点D的坐标;
(3)在(2)的条件下,将抛物线在点A,D之间的部分(含点A,D)记为图象G,如果图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.
【答案】(1)y=![]() x2﹣x+2;(2)C点坐标为(2,2);D点坐标为(4,6);(3)当1<t≤3时,图象G向下平移t(t>0)个单位后与直线BC只有一个公共点.
x2﹣x+2;(2)C点坐标为(2,2);D点坐标为(4,6);(3)当1<t≤3时,图象G向下平移t(t>0)个单位后与直线BC只有一个公共点.
【解析】
试题分析:(1)把A点和B点坐标代入![]() 得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)利用配方法得到y=![]() (x﹣1)2+
(x﹣1)2+![]() ,则抛物线的对称轴为直线x=1,利用点C与点A关于直线x=1对称得到C点坐标为(2,2);然后利用二次函数图象上点的坐标特征求D点坐标;
,则抛物线的对称轴为直线x=1,利用点C与点A关于直线x=1对称得到C点坐标为(2,2);然后利用二次函数图象上点的坐标特征求D点坐标;
(3)画出抛物线,如图,先利用待定系数法求出直线BC的解析式为y=![]() x+1,再利用平移的性质得到图象G向下平移1个单位时,点A在直线BC上;图象G向下平移3个单位时,点D在直线BC上,由于图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,所以1<t≤3.
x+1,再利用平移的性质得到图象G向下平移1个单位时,点A在直线BC上;图象G向下平移3个单位时,点D在直线BC上,由于图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,所以1<t≤3.
解:(1)把A(0,2)和B(1,![]() )代入
)代入![]() 得
得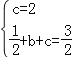 ,解得
,解得![]() ,
,
所以抛物线解析式为y=![]() x2﹣x+2;
x2﹣x+2;
(2)∵y=![]() x2﹣x+2=
x2﹣x+2=![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴抛物线的对称轴为直线x=1,
∵点C与点A关于此抛物线的对称轴对称,
∴C点坐标为(2,2);
当x=4时,y=![]() x2﹣x+2=8﹣4+2=6,
x2﹣x+2=8﹣4+2=6,
∴D点坐标为(4,6);
(3)如图,
设直线BC的解析式为y=mx+n,
把B(1,![]() ),C(2,2)代入得
),C(2,2)代入得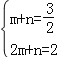 ,解得
,解得![]() ,
,
∴直线BC的解析式为y=![]() x+1,
x+1,
当x=0时,y=![]() x+1=1,
x+1=1,
∴点图象G向下平移1个单位时,点A在直线BC上,
当x=4时,y=![]() x+1=3,
x+1=3,
∴点图象G向下平移3个单位时,点D在直线BC上,
∴当1<t≤3时,图象G向下平移t(t>0)个单位后与直线BC只有一个公共点.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案