题目内容
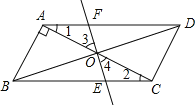
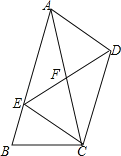
【题目】如图,在四边形ABCD中,AB∥CD,过点C作CE∥AD交AB于E,连接AC、DE,AC与DE交于点F.
(1)求证:四边形AECD为平行四边形;
(2)如果EF=2![]() ,∠FCD=30°,∠FDC=45°,求DC的长.
,∠FCD=30°,∠FDC=45°,求DC的长.
【答案】(1)见解析;(2)2+2![]() .
.
【解析】
试题分析:(1)由平行四边形的定义即可得出四边形AECD为平行四边形;
(2)作FM⊥CD于M,由平行四边形的性质得出DF=EF=2![]() ,由已知条件得出△DFM是等腰直角三角形,DM=FM=
,由已知条件得出△DFM是等腰直角三角形,DM=FM=![]() DF=2,由含30°角的直角三角形的性质和勾股定理得出CF=2FM=4,CM=2
DF=2,由含30°角的直角三角形的性质和勾股定理得出CF=2FM=4,CM=2![]() ,得出DC=DM+CM=2+2
,得出DC=DM+CM=2+2![]() 即可.
即可.
(1)证明:∵AB∥CD,CE∥AD,
∴四边形AECD为平行四边形;
(2)解:作FM⊥CD于M,如图所示:
则∠FND=∠FMC=90°,
∵四边形AECD为平行四边形,
∴DF=EF=2![]() ,
,
∵∠FCD=30°,∠FDC=45°,
∴△DFM是等腰直角三角形,
∴DM=FM=![]() DF=2,CF=2FM=4,
DF=2,CF=2FM=4,
∴CM=2![]() ,
,
∴DC=DM+CM=2+2![]() .
.


练习册系列答案
相关题目