题目内容
【题目】如图,在△ABC中,M是BC边的中点,AP平分∠A,BP⊥AP于点P、若AB=12,AC=22,则MP的长为_________.

【答案】5
【解析】先作辅助线,再根据三角形全等的性质得出BP=DB,再利用角平分线的性质计算.
解:延长BP与AC相交于D,延长MP与AB相交于E
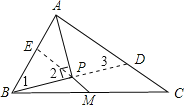
因为∠BAP=∠DAP,AP⊥BD,AP=AP
所以△ABP≌△APD
于是BP=PD
又∵M是BC边的中点
故PM∥AC
所以∠2=∠3
又因为∠1=∠3
所以∠1=∠2,EP=AE=![]() AB=
AB=![]() ×12=6
×12=6
AD=2EP=2×6=12
DC=22-12=10
PM=![]() DC=
DC=![]() ×10=5
×10=5
故MP的长为5.
故答案为5.
“点睛”本题比较复杂,考查的是三角形的中位线定理及角平分线的性质,解答此题的关键是延长BP与AC相交于D,延长MP与AB相交于E,构造出三角形,再解答.

练习册系列答案
相关题目


