题目内容
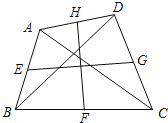
【题目】如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2=______.
【答案】36。
【解析】
连接EF,FG,GH,EH,由E、F、G、H分别是AB、BC、CD、DA的中点,得到EH,EF,FG,GH分别是△ABD,△ABC,△BCD,△ACD的中位线,根据三角形中位线定理得到EH,FG等于BD的一半,EF,GH等于AC的一半,由AC=BD=6,得到EH=EF=GH=FG=3,根据四边都相等的四边形是菱形,得到EFGH为菱形,然后根据菱形的性质得到EG⊥HF,且EG=2OE,FH=2OH,在Rt△OEH中,根据勾股定理得到OE2+OH2=EH2=9,再根据等式的性质,在等式的两边同时乘以4,根据4=22,把等式进行变形,并把EG=2OE,FH=2OH代入变形后的等式中,即可求出EG2+FH2的值
如图,连接EF,FG,GH,EH,

∵E、H分别是AB、DA的中点,
∴EH是△ABD的中位线,
∴EH=![]() BD=3,
BD=3,
同理可得EF,FG,GH分别是△ABC,△BCD,△ACD的中位线,
∴EF=GH=![]() AC=3,FG=
AC=3,FG=![]() BD=3,
BD=3,
∴EH=EF=GH=FG=3,
∴四边形EFGH为菱形,
∴EG⊥HF,且垂足为O,
∴EG=2OE,FH=2OH,
在Rt△OEH中,根据勾股定理得:OE2+OH2=EH2=9,
等式两边同时乘以4得:4OE2+4OH2=9×4=36,
∴(2OE)2+(2OH)2=36,
即EG2+FH2=36.
故答案为:36.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某儿童游乐园门票价格规定如下表:
购票张数 | 1~50张 | 51~100张 | 100张以上 |
每张票的价格 | 13元 | 11元 | 9元 |
某校七年级(1)、(2)两个班共102人今年6.1儿童节去游该游乐园,其中(1)班人数较少,不足50人。经估算,如果两个班都以班为单位购票,则一共应付1218元。问:
(1)两个班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可以节省多少钱?