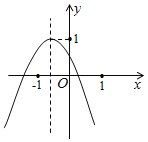题目内容
【题目】某校篮球队进行罚球练习,在 20 次罚球中,5 名首发运动员的进球数分别为 18,20,18,16,18,则对这 5 名运动员的成绩描述错误的是( )
A.众数为 18B.方差为 0C.中位数为 18D.平均数为 18
【答案】B
【解析】
根据众数、中位数、平均数和方差的定义和计算公式分别进行解答即可.
∵18 出现了 3 次,出现的次数最多,
∴众数为 18,
故 A 本选项正确;
这组数据的平均数是(18+20+18+16+18)÷5=18,
则方差为 S2=![]() [(18-18)2+(20-18)2+(18-18)2+(16-18)2+(18-18)2]=1.6,故 B 选项错误,D 选项正确;
[(18-18)2+(20-18)2+(18-18)2+(16-18)2+(18-18)2]=1.6,故 B 选项错误,D 选项正确;
把这些数从小到大排列为 16,18,18,18,20,最中间的数是 18, 则中位数是 18,
故 C 选项正确;
则对这 5 名运动员的成绩描述错误的是 B;
故选:B.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
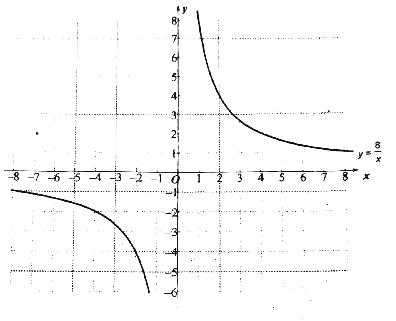
【题目】某班数学兴趣小组根据学习函数的经验,通过列表、描点、连线的方法对函数 y=![]() 的图象与性质进行了研究,研究过程如下,请补充完整.
的图象与性质进行了研究,研究过程如下,请补充完整.
(1)y 与 x 的几组对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | … |
y | … |
|
| 6 | 6 | m |
| … |
函数 y=![]() 的自变量 x 的取值范围是 ,m 的值为 ;
的自变量 x 的取值范围是 ,m 的值为 ;
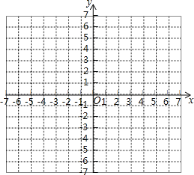
(2)在给出的平面直角坐标系中,描出以上表中各组对应值为坐标的点,画出函数 y=![]() 的大致图象,并写出该函数的两条性质;
的大致图象,并写出该函数的两条性质;
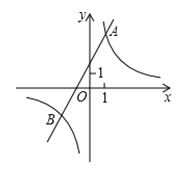
(3)在同一坐标系中画出函数 y1=![]() x 的图象,并根据图象直接写出当 y>y1 时,自变量 x 的取值范围.
x 的图象,并根据图象直接写出当 y>y1 时,自变量 x 的取值范围.