Question

【题目】点E在射线OA上，点F在射线OB 上，AO⊥BO，EM平分∠AEF，FM平分∠BFE，则tan∠EMF的值为( )

A.B.C.1D.

Answer 1

【答案】C

【解析】

根据三角形外角的性质求得∠AEF+∠BFE=270°，由角平分线定义可求得∠MEF+∠MFE=135°，根据三角形内角和定理可求出∠EMF=45°，从而可得出结论．

如图，

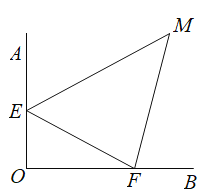
∵AO⊥BO

∴∠AOB=90°

∴∠OEF+∠OFE=90°

∵∠AEF和∠BFE是△EOF的外角

∴∠AEF=90°+∠OFE，∠BFE=90°+∠OEF

∴∠AEF+∠BFE=90°+90°+∠OFE+∠OEF=270°

∵EM平分∠AEF，FM平分∠BFE，

∴∠MEF+∠MFE=(∠AEF+∠BFE) =135°，

∵∠MEF+∠MFE+∠M=180°

∴∠M=180°-(∠MEF+∠MFE)=180°-135°=45°

∴tan∠EMF=tan45°=1

故选：C．